CHUYỆN ĐÂU ĐÂU: Shapiro – Suy Nghĩ Về Toán Học (04)

Suy Nghĩ Về Toán Học

(Triết Học của Toán Học)

Stewart Shapiro

NHỮNG ĐỐI LẬP GẦN: KANT VÀ MILL

1. Định hướng lại

Chúng ta tiếp tục câu chuyện còn dở dang của chúng ta trong thế kỷ 18, với Immanuel Kant. Tất nhiên, đã có hoạt động triết học đáng kể trong thời Cổ, sau Aristotle và qua thời Trung cổ, nhưng nó đã không nhiều tập trung trực tiếp trên toán học.[1]

Thế kỷ 17 đã thấy những cách mạng lớn trong khoa học và toán học, qua những người như Rene Descartes, Isaac Newton và Gottfried Wilhelm Leibniz. Kant đã trong một vị trí để nhận lấy sự đo lường triết học của những phát triển khoa học mới. Những đòi hỏi của vật lý đang nổi lên đã dẫn đến sự phát triển của những nhánh toán học mới và đến những khái niệm mới của những nhánh toán học truyền thống. Những sáng kiến chủ yếu gồm những phương pháp mới của toán phân tích liên kết hình học với đại số học và số học (Pierre Fermat và Descartes), và sự phát triển của calculus (Newton và Leibniz) cho sự nghiên cứu của lực hấp dẫn và chuyển động. Nghiên cứu vừa kể sau đòi hỏi những khái niệm về liên tục, đạo hàm và giới hạn, trong số đó không khái niệm nào đặt vừa vặn được vào trong những mô hình toán học trước đó. (Xem Mancosu 1996 cho một giải quyết minh bạch về toán học và triết học của nó trong thế kỷ 17).

Ở thời đó, có hai trường phái triết học lớn. Trên lục địa Europe, những người theo thuyết duy lý như Descartes, Baruch Spinoza và Leibniz đã là những người thừa kế tự nhiên của Plato. Họ đã nhấn mạnh vai trò của lý trí, như đối lại với kinh nghiệm giác quan, trong việc thu nhận kiến thức. Những dạng cực đoan của cái nhìn này tuyên bố rằng tất cả kiến thức, hoặc trong lý tưởng, phải là dựa trên lý trí. Mô hình duy lý cho việc thu thập kiến thức là toán học – đặc biệt là chứng minh toán học. Thí dụ: Ethics của Spinoza có cùng hình thức như Elements của Euclid, chứa ‘những mệnh đề’ và ‘những chứng minh’. Phần lớn công trình triết học của Descartes là một cố gắng để đem cho khoa học cùng mức độ của chắc chắn như toán học. Khoa học thì giả định là được thành lập trên những nguyên lý đầu tiên của triết học [2]. Descartes đã gắng thử một suy diễn theo kiểu toán học của những luật của chuyển động. [3]

Thuyết duy nghiệm, đối lập chính với thuyết duy lý, là một cố gắng để dựa kiến thức, hay những vật liệu từ đó kiến thức đã dựa vào chúng, trên kinh nghiệm từ năm giác quan. Trong giai đoạn đang bàn, những người viết lớn là John Locke, George Berkeley, David Hume và Thomas Reid, tất cả họ đều sống ở quần đảo Britain, Một chủ đề duy nghiệm phổ thông là bất cứ gì chúng ta biết về thế giới phải cuối cùng đều đến từ sự quan sát trung lập và lãnh đạm. Sự tiếp cận duy nhất với vũ trụ là qua tai, mắt, v.v. của chúng ta. Những người theo thuyết duy nghiệm đôi khi trình bày một hình ảnh của não thức như một tấm bảng trắng, trên đó thông tin được in sâu, qua những giác quan. Chúng ta là những người quan sát thụ động, sàng lọc qua những dữ liệu đi đến, cố gắng để tìm hiểu ý nghĩa của thế giới xung quanh chúng ta.

Không có giải thích triết học chi tiết quan trọng nào đáng kể về toán học trong giai đoạn này. Tất nhiên, những người theo thuyết duy lý, đã ngưỡng mộ toán học, và chính những Descartes và Leibniz đều là những nhà toán học lớn. Những người theo thuyết duy nghiệm có khuynh hướng hạ thấp sự quan trọng của toán học, có lẽ vì nó không phù hợp dễ dàng với khuôn mẫu thu thập kiến thức của họ. Berkeley đã khởi động một tấn công kéo dài trên sự chính xác nghiêm ngặt được giả định của calculus về sự thay đổi liên tục. [4] (xem Jesseph 1993). Tuy nhiên, trước vai trò của toán học trong những ngành khoa học, những người theo thuyết duy nghiệm phải đưa ra một số giải thích về nó.

Những nhận xét triết học rải rác về toán học ngạc nhiên cho thấy một lượng đồng ý lớn giữa hai trường phái lớn. Cả những người theo thuyết duy lý và những người theo thuyết duy nghiệm đều coi toán học là về những độ lớn vật lý, hay những đối tượng mở rộng. Những đối tượng đã tiếp xúc qua kinh nghiệm. Hai trường phái khác nhau trên sự tiếp cận của não thức với những ý tưởng của những đối tượng mở rộng và về trạng thái của việc suy luận về những ý tưởng đó. Thí dụ, Descartes chủ trương rằng chúng ta có nhận thức rõ ràng và phân biệt về phần mở rộng thuần túy vốn ẩn chìm trong những đối tượng vật chất, và ông chủ trương rằng chúng ta có thể lý luận trực tiếp về phần mở rộng thuần túy này. Cái nhìn này chứng thực xác quyết duy lý rằng trí tuệ con người là một dụng cụ đắc lực cho việc lý luận – về toán học – đem hỗ trợ quan trọng cho những kết luận tiên nghiệm về thế giới vật lý.

Những người theo thuyết duy nghiệm đã nhận những ý tưởng toán học là đã bắt nguồn từ kinh nghiệm, có lẽ đi theo Aristotle. Thí dụ, ý tưởng của chúng ta về số 6, đến từ kinh nghiệm của chúng ta với những nhóm gồm 6 đối tượng. Ý tưởng của ‘hình tam giác’ đến từ việc nhìn vào những vật thể hình-tam giác. Với người theo thuyết duy nghiệm, không có “sự mở rộng thuần túy” thực chất nào ẩn chìm trong những đối được tri giác. Chỉ có những đối tượng được tri giác. Những gì bạn trông thấy là những gì bạn có được.

Mặc dù những điều này và những khác biệt khác, một người theo thuyết duy nghiệm điển hình có thể đồng ý với một người theo thuyết duy lý điển hình rằng, một khi có được những ý tưởng liên quan, sự theo đuổi kiến thức toán học thì độc lập với bất kỳ kinh nghiệm thêm hơn nào khác. Nhà toán học suy ngẫm tìm xem những ý tưởng toán học khác nhau liên quan với nhau thế nào. Thí dụ, trong Treatise on Human Nature, Hume nhắc đến những đúng thật của số học và đại số học như ‘những quan hệ của những ý tưởng’ và phân biệt chúng với ‘những sự vật việc của thực tế và hiện hữu’, vốn chúng ta học biết qua kinh nghiệm [5]. Hình học là một khoa học duy nghiệm, đã giả định có quan tâm với những khái quát hóa từ kinh nghiệm. Mười năm sau, trong quyển An Enquiry Concerning Human Understanding phổ thông của ông, Hume tuyên bố rằng số học, đại số học và hình học đều tất giống nhau, chúng đều (đơn thuần) quan tâm với những quan hệ giữa những ý tưởng, và do đó chúng không là duy nghiệm. Nền tảng chung giữa những trường phái, ít nhất trong một ý hướng nào đó, là những đúng thật toán học là tiên nghiệm, hay độc lập với kinh nghiệm. Tranh luận chính là cho đến mức độ nào kinh nghiệm giác quan thì cần thiết để có được hay thấu hiểu những ý tưởng liên quan và để nghiên cứu chúng.

Sự đúng thật trong toán học ít nhất hiện ra như có một tất yếu nhất định nào đó đã gắn với nó. Trong điều kiện nào 5 + 7 có thể không là 12? Định lý lấy thừa số nguyên tố có thể sai như thế nào? Thuyết duy lý đem cho một giải thích suông sẻ về điều này, dọc những đường suy nghĩ ‘gập ghềnh’ theo Plato. Không có bất ngờ hay ngẫu sinh nào trong những ý tưởng toán học nắm bắt được về tinh thần, giống như sự mở rộng thuần túy, vốn nằm chìm dưới những đối tượng vật lý. Tất nhiên, chúng ta có thể sai lầm trong nắm bắt của chúng ta về những ý tưởng toán học hay trong gắng thử một bằng chứng, nhưng, nếu được thực hiện đúng cách, phương pháp luận của toán học mang lại chỉ những đúng thật tất yếu. Tất nhiên viễn tượng này không dành cho những người theo thuyết duy nghiệm, và họ không có một giải thích rõ ràng dễ hiểu như vậy về tính tất yếu dường có của toán học. Một số họ có thể chủ trương rằng những mệnh đề toán học cơ bản là đúng theo định nghĩa, một kết luận vốn một người theo thuyết duy lý sẽ cảm thấy thất vọng vì nó bỏ lại toán học với không thực chất. Hume lưu ý rằng chúng ta không thể tưởng tượng hay khai triển một ý niệm về những phủ định của những định lý toán học điển hình, nhưng điều này xem dường như là một chủ trương yếu trên tính tất yếu của toán học. Có phải chỉ một sự giới hạn tâm lý ngẫu nhiên vốn ngăn cản chúng ta với việc hình dung những sự vật việc trong bất kỳ cách nào khác?

Việc dùng toán học mới trong khoa học đã mang đến sức mạnh mới cho những vấn đề của tính ứng dụng của toán học với thế giới vật lý. Ở đây thuyết duy nghiệm đã làm tốt hơn. Theo trường phái đó, những ý tưởng toán học được ‘đọc ra’ khỏi những thuộc tính của những đối tượng đã quan sát, và những nhà toán học nghiên cứu những quan hệ giữa những ý tưởng này. Đó là, những người theo thuyết duy nghiệm chủ trương rằng nhà toán học nghiên cứu gián tiếp những quan hệ vật lý nhất định nào đó giữa những đối tượng vật lý đã quan sát. Giải thích này thì không có sẵn sàng với một người theo thuyết duy lý. Vấn đề của người này là để cho thấy những thực thể toán học vĩnh cửu, nắm bắt bẩm sinh có liên hệ thế nào với những đối tượng chúng ta tri giác trong thế giới quanh chúng ta, và nghiên cứu trong khoa học. Do đó, người theo thuyết duy nghiệm của chúng ta đi theo Aristotle, với một giải thích rõ ràng không khúc mắc về sự tương ứng giữa những đối tượng vật lý được quan sát và những tương ứng của chúng, trong khi người theo thuyết duy lý của chúng ta đi theo Plato, với một giải thích đơn giản về sự không tương ứng giữa những đối tượng của giác quan và những tương ứng toán học của chúng, như những vòng tròn và hình tam giác toàn hảo, và có lẽ những con số lớn.

2. Kant

Sự xung đột giữa thuyết duy lý và thuyết duy nghiệm đem đến một động lực trung tâm cho cố gắng của Kant trong một tổng hợp vốn thâu tóm những khía cạnh đặc biệt giá trị nhất của mỗi thuyết. Kết quả đã là một cố gắng hào hùng để giải thích hay cung cấp không gian cho tính tất yếu của toán học và bản chất tiên nghiệm của đúng thật toán học, trong khi giải thích hay đem cho vị trí của toán học trong khoa học thực nghiệm và đặc biệt trong tính có thể ứng dụng của toán học với thế giới vật lý được quan sát. Vấn đề của Kant đã là để cho thấy toán học có thể biết được tiên nghiệm như thế nào, và lại vẫn áp dụng được phổ quát – cho tất cả kinh nghiệm – với sự chắc chắn không thể sửa chữa được. Những cái nhìn của ông về toán học không là một thành phần tách rời của toàn bô triết học của ông. Ngược lại, những nhắc dẫn toán học diễn ra suốt trong mọi văn bản triết học của ông. Thế nên, một chìa khóa quan trọng để hiểu Kant là để hiểu những cái nhìn của ông trên toán học.

Người đọc nên lưu ý rằng, ngay cả nếu phác lược sau đây quả thực có nêu lên một vài chủ đề của triết học của toán học phức tạp và tinh tế của Kant, nó mới chỉ là những ‘cào xước’ (bàn luận thiếu chiều sâu) ngoài mặt. Hơn nữa, có nhiều những bất đồng giữa những học giả (xem những mục được nói đến ở cuối chương này, để bắt đầu). Những diễn giải tạm nêu lên dưới đây dựa trên một số công trình của họ, và tôi đã cố gắng hoặc ghi nhận những bất đồng chính hoặc tránh xa khỏi chúng. Tuy nhiên, không thể tránh được rằng những phần của một diễn giải bất kỳ nào sẽ bất đồng với một số nghiên cứu học thuật chú ý nổi bật.

Đặc điểm lôi cuốn và khó khăn nhất trong triết học của toán học của Kant là luận điểm của ông rằng sự đúng thật của hình học, số học và đại số là ‘tổng hợp tiên nghiệm’, được thành lập trên ‘trực giác’. Thế nên, những khái niệm then chốt là kiến thức tiên nghiệm, sự phân biệt tương phản phân tích-tổng hợp và khả năng của trực giác.

Đối với Kant, một mệnh đề phổ quát (trong dạng ‘Mọi S đều là P’) là phân tích nếu khái niệm vị ngữ (P) thì chứa trong khái niệm chủ ngữ (S); nếu không thì mệnh đề là tổng hợp. Thí dụ, ‘tất cả những người độc thân đều chưa-lập gia đình’ là phân tích nếu khái niệm chưa-lập gia đình thì có trong khái niệm của người độc thân. ‘Tất cả mọi người đều chết’ là phân tích nếu khái niệm chết thì có trong khái niệm con người. Vì là phái nam (có lẽ) không là phần của khái niệm của làm Tổng thống, nên ‘tất cả những Tổng thống là phái nam’ là tổng hợp.

Như bây giờ chúng ta biết, không phải mọi mệnh đề đều có một dạng chủ ngữ – vị ngữ, và do đó, nhìn dưới ánh sáng thời nay, định nghĩa về phân tích của Kant là không-tự nhiên và kìm hãm ngột ngạt. Ông có nhìn nhận những dạng khác của phán đoán, sau khi đề nghị rằng sự áp dụng của sự phân biệt phân tích-tổng hợp với những phán đoán phủ định thì đơn giản (Critique of Pure Reason, A6 / Bl 1), nhưng ông không nói gì khác nhiều. Thế còn những mệnh đề giả thuyết như ‘nếu bây giờ trời đang mưa, thì hoặc trời đang mưa hoặc trời đang có mưa tuyết? Đây không là chỗ để đề nghị những cải tiến hay những mở rộng của sự phân biệt của Kant, nhưng chúng ta cần phải xem xét cơ bản của nó. [6]

Vị thế siêu hình của phân tích những đúng thật của Kant mở ra bản chất của những khái niệm. Chúng ta không cần đào sâu hơn vào trong điều này, ngoài việc lưu ý rằng luận điểm của Kant có giả định-trước rằng khái niệm có những phần (ít nhất là theo nghĩa ẩn dụ), vì nếu không thì chúng ta không thể nói về một khái niệm ‘chứa đựng’ một khái niệm khác. Những vấn đề liên quan ở đây là tri thức học. Kant tin rằng những phần của khái niệm được nắm bắt qua một tiến trình tâm lý của phân tích khái niệm. Thí dụ, khi trình bày một mệnh đề trong ở dạng ‘Tất cả S là P’, chúng ta phân tích khái niệm chủ ngữ S để xem vị ngữ P có nằm trong số những phần hay không. Chúng ta biết rằng tất cả ‘những người độc thân đều chưa lập gia đình’ bằng việc phân tích người độc thân và biết rằng nó có chứa ‘chưa lập gia đình’. Vắn tắt, bất kể khái niệm là gì, Kant chủ trương rằng bất kỳ một ai nắm giữ một khái niệm thì trong một vị thế để thực hiện sự phân tích và xác định những thành phần của nó. Phân tích khái niệm khai quật được những gì đã ẩn chìm trong những khái niệm: Những phán đoán phân tích ... có thể được gọi là làm sáng tỏ. Vì chúng không qua vị ngữ để thêm bất cứ gì vào khái niệm của chủ ngữ; đúng hơn chúng chỉ mổ xẻ khái niệm, chia nhỏ nó thành những khái niệm thành phần, vốn đã được nghĩ trong nó rồi (Critique of Pure Reason, B11). Vì vậy, phân tích khái niệm không mang lại kiến thức mới về thế giới. Theo một ý hướng nào đó, nó không bảo cho chúng ta biết gì cả, hay không có gì mới.

Điều là đơn giản dễ hiểu rằng những đúng thật phân tích đều là biết được tiên nghiệm. Cho A là một đúng thật phân tích. Bất cứ ai nắm được những khái niệm trình bày trong A thì trong một vị trí để xác định những phần của chúng và do đó sự đúng thật của A. Không cần thiết có kinh nghiệm cụ thể nào về thế giới, ngoài những gì cần thiết để nắm được những khái niệm tất yếu.

Kant lưu ý rằng một số ít những mệnh đề toán học là phân tích. Thí dụ, hãy xem xét ‘tất cả những tam giác đều có ba góc’ hay có lẽ ‘tất cả những tam giác đều có ba cạnh’ [7], hay ‘tất cả những tam giác đều đồng dạng’. Tuy nhiên, Kant chủ trương rằng hầu hết tất cả những mệnh đề toán học đều là tổng hợp. Phân tích khái niệm, chỉ mình nó, thì không xác định rằng ‘7 + 5 = 12’, hay ‘giữa hai điểm bất kỳ có thể vẽ được một đường thẳng x’, hay rằng ‘một đường thẳng là khoảng cách ngắn nhất giữa hai điểm’. Xem xét những khái niệm tương ứng với 7, 5, 12, phép cộng, định tính, điểm và đường thẳng sẽ không mở ra sự đúng thật của những mệnh đề này.

Để thấy tại sao Kant đã nghĩ rằng phân tích khái niệm thì không đủ để thiết lập nhiều những mệnh đề toán học, chúng ta chú ý tới tri thức học của Kant. Ông chủ trương rằng những mệnh đề tổng hợp đều có thể biết được chỉ qua ‘trực giác’, và vì vậy chúng ta phải quay sang khái niệm đó.

Trực giác theo Kant có hai thuộc tính đặc biệt, dù những học giả không đồng ý về sự quan trọng tương đối của mỗi chúng. Đầu tiên, trực giác là cá biệt/đơn lẻ, trong ý hướng rằng chúng là những phương thức của việc hình dung cho những đối tượng cá biệt. Thật vậy, trực giác là thiết yếu cho kiến thức của những đối tượng cá biệt. Ngược lại, phân tích khái niệm thì không cá biệt, và chỉ đưa ra những sự đúng thật tổng quát. Chúng ta biết từ phân tích khái niệm, rằng tất cả những người độc thân đều chưa lập gia đình, nhưng bằng cách đó chúng ta không biết có bất kỳ những người độc thân nào hay không, cũng không quen biết với bất kỳ một người độc thân nào. Trong bàn luận về luận chứng bản thể học cho sự hiện hữu của Gót, Kant biện luận rằng chúng ta không thể tìm hiểu về sự hiện hữu của bất cứ gì chỉ bằng sự phân tích khái niệm mà thôi (Critique of Pure Reason, B622-3). Để điều chỉnh luận điểm này với toán học, giả đỉnh rằng một ai đó muốn chứng minh rằng có một số nguyên tố lớn hơn 100. Theo cách thức điển hình toán học, người ấy giả định rằng mọi số tự nhiên trên 100 đều là những hợp số (số nguyên có nhiều hơn hai ước số) và dẫn đến một mâu thuẫn. Vì vậy, có lẽ người ấy đã thiết lập một đúng thật phân tích rằng không là trường hợp xảy ra rằng tất cả những số trên 100 đều là những hợp số. Nhưng chúng ta chỉ nhận được sự hiện hữu của một số nguyên tố nếu chúng ta biết rằng có những số tự nhiên lớn hơn 100. Trong chừng mức của phân tích khái niệm, có vẻ như chúng ta vẫn có lựa chọn để bác bỏ giả thiết về hiện hữu. [8] Tương tự, chúng ta chỉ biết rằng một đường chéo của một hình vuông là không so sánh tỉ lệ [9] với cạnh của nó, nếu chúng ta biết rằng có những hình vuông và những hình vuông có những đường chéo. Phân tích khái niệm không thiết lập điều này. Theo Kant, chúng ta cần trực giác để hình dung, trình bày những con số (hay những nhóm đối tượng được đánh số) và những dạng hình học, và để tìm hiểu những sự việc về chúng. Huống chi, phân tích khái niệm không thể đem cho (tiềm năng) vô hạn của số và của không gian (xem Friedman 1985).

Vì vậy, một lý do để coi toán học là tổng hợp là nó giải quyết những đối tượng đơn lẻ như những nhóm của những sự vật việc đã đánh số, những dạng hình học, và ngay cả tự thân không gian – vốn Kant coi là đặc biệt độc nhất, và thấu hiểu được bằng trực giác. Tuy nhiên, những quan điểm của ông sâu xa hơn điều này.

Trong một đoạn văn nổi tiếng, hay tai tiếng, Kant lập luận rằng những tổng số là tổng hợp:

Đúng là thoạt đầu một người có thể nghĩ rằng mệnh đề 7 + 5 = 12 là một phân tích đơn thuần, bởi nguyên lý mâu thuẫn, từ khái niệm của một tổng số bảy và năm. Tuy nhiên, nếu chúng ta nhìn kỹ hơn; chúng ta thấy rằng khái niệm của tổng số của 7 và 5 chứa không gì hơn là sự hợp nhất của hai con số vào thành một; nhưng trong [suy nghĩ] về hợp nhất đó, chúng ta hoàn toàn không nghĩ gì cả rằng con số duy nhất đó vốn hợp nhất cả hai là gì. Trong suy nghĩ chỉ đơn thuần về sự hợp nhất của bảy và năm, tôi hoàn toàn không có cách nào đã nghĩ đến khái niệm mười hai; và cho dù tôi có mổ xẻ khái niệm của tôi về một tổng số có thể có như vậy trong bao lâu, tôi vẫn sẽ không bao giờ tìm thấy trong đó con số mười hai. Chúng ta phải vượt ra khỏi những khái niệm này và tận dụng chúng ta với trực giác tương ứng với một trong hai: ví dụ: năm ngón tay của chúng ta hoặc ... năm dấu chấm. Trong cách này, chúng ta phải dần dần cộng them, vào khái niệm của số bảy, những đơn vị của năm được cho trong trực giác ... Trong cách này, tôi thấy số 12 xuất hiện. Số 5 đó được cộng với 7, điều này tôi quả thực đã nghĩ trong khái niệm của một tổng số = 7 + 5, nhưng không phải rằng tổng số này bằng với số 12. Do đó, những mệnh đề số học luôn là tổng hợp. Chúng ta nhận thức rõ ràng hơn về điều này nếu chúng ta lấy những số lớn hơn. Vì khi đó, là điều rất hiển nhiên rằng. . . chúng ta không bao giờ có thể tìm thấy. . . tổng số bằng chỉ đơn thuần mổ xẻ những khái niệm của chúng ta, tức là, không tự tận dụng trực giác chúng ta. (Critique of Pure Reason, B15-16)

Nhớ lại rằng với Kant phân tích khái niệm không mang lại kiến thức mới. Đúng hơn, nó chỉ mở ra cho thấy những gì ẩn chìm trong những khái niệm. Ở đây Kant khẳng định rằng phép cộng mang lại kiến thức mới, và cũng thế là sự tổng hợp.

Kant chủ trương rằng, mặc dù hầu hết những mệnh đề toán học là tổng hợp, chúng đều được biết tiên nghiệm, độc lập với kinh nghiệm giác quan. Điều này có thể là thế nào? Cho dù động lực đến từ toán học hay không, phần lớn triết học tổng quát của Kant thì được dành để cho thấy những mệnh đề tiên nghiệm tổng hợp có thể thực hiện được thế nào. Làm thế nào có thể có những đúng thật tiên nghiệm vốn không đặt nền tảng trong phân tích khái niệm?

Một đăc điểm thứ hai của trực giác theo Kant là nó đem đến kiến thức trực tiếp. Như đã cho thấy trong đoạn văn về 7 + 5, ít nhất với con người, trực giác thì gắn buộc với tri thức giác quan. Một trực giác điển hình sẽ là nhận thức vốn làm nền tảng cho phán đoán rằng bàn tay phải của tôi có năm ngón tay.

Tất nhiên, trực giác loại này thì thực nghiệm và kiến thức nó tạo ra thì tùy thuộc [10]. Chúng ta không học toán theo cách đó. Kant chủ trương rằng có một dạng trực giác mang lại kiến thức tiên nghiệm của những đúng thật tất yếu. Trực giác ‘thuần túy’ này giao cho những dạng của những trực giác duy nghiệm có thể có. Nghĩa là, trực giác thuần túy là một ý thức về hình thức không-thời [11] của tri thức giác quan thông thường. Ý tưởng là trực giác thuần túy mở ra cho thấy những giả định -trước của kiến thức thực nghiệm, không phức tạp rắc rối của những đối tượng không-thời. Thí dụ, hình học Euclid liên quan đến cách con người tất yếu nhận thức không gian và những đối tượng không gian. Chúng ta nắm bắt những đối tượng trong không gian ba chiều, những vùng bao quanh với những đường thẳng, v.v. Số học liên quan đến cách con người nhận thức những đối tượng trong không gian và thời gian, xác định vị trí và phân biệt những đối tượng và đếm chúng. Do đó, số học và hình học mô tả khung cấu trúc hỗ trợ của nhận thức. Như Jaakko Hintikka (1967: §18) đã nói, với Kant, ‘sự hiện hữu của những riêng lẻ [12] vốn lý luận toán học quan tâm với chúng là nhờ vào tiến trình của nó chúng ta đi đến biết sự hiện hữu của những riêng lẻ trong tổng quát. Kant chủ trương rằng tiến trình này là nhận thức giác quan. Vì vậy, cấu trúc của lý luận toán học là nhờ vào cấu trúc của bộ máy nhận thức của chúng ta’.

Nhớ lại rằng, với Descartes, ‘mở rộng thuần túy’ được nhận thức trực tiếp trong những đối tượng vật lý (ít nhất về nghĩa ẩn dụ). Ngược lại, Kant lấy trực giác thuần túy để quan tâm với những dạng nhận thức có thể có của con người. Những dạng này không trong những đối tượng vật lý tự thân, nhưng trong một ý hướng nào đó, chúng được não thức con người cung cấp. Chúng ta cấu trúc những nhận thức của chúng ta trong một cách thức nhất định nào đó

Đây là một đoạn từ Critique of Pure Reason, làm nổi bật bản chất của trực giác tiên nghiệm hình học và tính tất yếu của toán học. Rõ ràng, Kant coi triết học là hoạt động của phân tích khái niệm, và ông nêu một sự tương phản với toán học:

Toán học đem cho thí dụ lộng lẫy nhất của một lý trí thuần túy tự mở rộng thành công trên chính nó, không với sự giúp đỡ của kinh nghiệm ... Nhận thức triết học là nhận thức duy lý từ những khái niệm. Nhận thức toán học là nhận thức duy lý từ sự xây dựng của những khái niệm. Nhưng để xây dựng một khái niệm nghĩa là để trưng bày trực giác tiên nghiệm tương ứng với nó. Do đó, sự xây dựng một khái niệm đòi hỏi một trực giác không-thực nghiệm.

Hệ quả là trực giác này, như trực giác, là một đối tượng riêng lẻ; nhưng như sự xây dựng của một khái niệm (một trưng bày phổ quát), nó dù sao cũng phải truyền đạt ... tính hợp lệ phổ quát của nó cho tất cả những trực giác có thể có thuộc cùng khái niệm. Thế nên, tôi xây dựng một tam giác bằng việc trưng bày đối tượng tương ứng với khái niệm này, hoặc qua chỉ tưởng tượng trong trực giác thuần túy hoặc... cũng trên giấy, và do đó cũng trong trực giác duy nghiệm. Nhưng trong cả hai trường hợp, tôi đều trưng bày đối tượng hoàn toàn tiên nghiệm, đã không lấy mô hình cho nó từ bất kỳ kinh nghiệm nào. Hình vẽ riêng lẻ được vẽ ở đó là thực nghiệm, nhưng vẫn dung để thể hiện khái niệm nhưng không làm yếu đi tính phổ quát của khái niệm. Đối với việc giải quyết trực giác duy nghiệm này, người ta chỉ tính đến hành động của việc xây dựng khái niệm – với nó nhiều những xác định là ... không quan trọng: thí dụ, độ lớn của những cạnh và của những góc – và do đó, một người tóm tắt từ những sự khác biệt đó vốn không thay đổi khái niệm của tam giác ... Tri thức triết học suy ngẫm cái riêng lẻ chỉ trong cái phổ quát. Mặt khác, tri thức toán học suy ngẫm về cái phổ quát trong ... cái riêng lẻ; tuy nhiên nó vẫn làm như vậy là tiên nghiệm và bằng phương tiện của lý trí. (Critique of Pure Reason, B741-2)

Như thế, chúng ta gặp một chủ đề được lập lại nhiều lần trong lịch sử triết học của toán học, sự trừu tượng hóa (xem chương 3, §4).

Người ta có thể nghĩ về trực giác thuần túy của Kant và tiến trình của trừu tượng hóa như việc trưng bày những trường hợp điển hình hay những mô thức của những khái niệm đã cho. Thí dụ, bắt đầu với khái niệm của tam giác, trực giác đem cho cho chúng ta (tiên nghiệm) một tam giác điển hình. Tương tự, bắt đầu với khái niệm của con số, trực giác đem cho một con số điển hình. Sau việc này, nhà toán học làm việc với những trường hợp đã trực giác. Tuy nhiên, như đã cho thấy ở cuối đoạn văn, đây có lẽ không là những gì Kant đã nghĩ. Có thể có một điểm hay đường thẳng điển hình, nhưng đơn giản là không có tam giác điển hình hay mô thức điển hình. Bất kỳ tam giác nào cho trước, dù được tưởng tượng hay trên giấy, phải là hoặc nhọn, vuông hay tù, và hoặc lệch, cân hay đều, và vì vậy bất kỳ tam giác nào đã cho không thể đại diện cho tất cả những tam giác. Hơn nữa, như Gottlob Frege (1884: §13) sau này đã cho thấy, sự trừu tượng thô giản này không có một cơ hội ứng dụng thành công vào số học. Mỗi số tự nhiên có những đặc tính riêng của nó và chỉ mình nó, và do đó không có số tự nhiên nào có thể đại diện cho tất cả những số tự nhiên.

Nhận xét của Kant rằng ‘trong việc giải quyết [một] trực giác duy nghiệm, người ta tính chỉ hành động của việc xây dựng khái niệm’, cho thấy một liên kết với một kỹ thuật phổ thông trong suy luận diễn dịch. Giả định rằng một nhà hình học làm một minh chứng hình học về những tam giác cân. Người ấy vẽ một hình tam giác như vậy và lý luận với nó. Trong bản văn tiếp theo, nhà hình học của chúng ta chỉ gọi những thuộc tính của tất cả những tam giác cân và không dùng bất kỳ đặc trưng nào khác của tam giác đã vẽ, chẳng hạn như kích thước chính xác của những góc hay liệu cạnh đáy thì ngắn hơn hay dài hơn những cạnh khác. Nếu thành công, kết luận giữ đúng cho tất cả những tam giác cân. Kỹ thuật này thì phổ thông trong toán học. Một nhà lý thuyết số học có thể bắt đầu ‘cho n là một số nguyên tố’ và tiếp tục suy luận với ‘thí dụ’ n, dùng chỉ những thuộc tính vốn đúng với tất cả những số nguyên tố. Nếu người ấy cho thấy rằng n có thuộc tính P, người ấy kết luận rằng tất cả những số nguyên tố đều có thuộc tính P, có lẽ nhắc nhở người đọc rằng n là ‘tùy tiện’.

Thực hành này tương ứng với một quy tắc của suy diễn trong những hệ thống lôgích thời nay, đôi khi được gọi là ‘tổng quát hóa’ hay ‘giới thiệu phổ quát’[13]. Trong những hệ thống của diễn dịch tự nhiên, quy tắc là từ một công thức trong dạng Φ (c) (tức là một vị từ Φ giữ đúng của một riêng lẻ c) người ta có thể suy ra ∀ x Φ (x) (tức là Φ giữ đúng của mọi sự vật việc), với điều kiện là hằng số c không xuất hiện trong công thức ∀ x Φ (x) hay trong bất kỳ tiền đề nào vốn Φ (c) dựa trên. Những hạn chế trong việc dùng quy tắc bảo đảm rằng thuật ngữ riêng lẻ c thực sự là tùy tiện bất kỳ. Nó có thể là bất kỳ số nào. Tuy nhiên, quy tắc suy diễn này nằm ngoài phạm vi lôgích như Kant đã biết. Kant nổi tiếng khẳng định rằng lôgích học không cần phải vượt quá những phương pháp suy luận (tam đoạn luận) của Aristotle. Khi giải thích Kant, Hintikka (1967) coi ‘những suy diễn’ giống như quy tắc tổng quát hóa là thành phần thiết yếu của trực giác toán học. Có nghĩa là, bất kỳ minh chứng nào vốn thiết yếu dung quy tắc này đều có một kết luận tổng hợp – ngay cả nếu những tiền đề của nó là phân tích. Trong những khung cấu trúc hỗ trợ thời nay, quy tắc tổng quát hóa gợi dậy một thuật ngữ riêng lẻ, hằng số ‘tùy tiện’ được đưa vào bản văn. Sau một thịnh hành, điều này phù hợp đặc điểm vốn trực giác của Kant đối phó với những đối tượng riêng lẻ. Theo cách giải thích này, nếu Kant đã học một số lôgích học thời nay, ông sẽ hoặc rút lại luận điểm chính của ông rằng toán học là tổng hợp, hoặc, nhiều phần xảy ra hơn, ông sẽ tuyên bố rằng dưới ánh sáng của lôgích (của chúng ta), một suy diễn hợp lệ có thể có những tiền đề phân tích. và một kết luận tổng hợp, chỉ vì một trong những quy tắc suy luận của chúng ta gợi dậy một thuật ngữ riêng lẻ (xem thêm chú thích 3 ở trên).

Tất nhiên, Kant đã buộc trực giác với nhận thức giác quan hoặc, trong trường hợp trực giác thuần túy, với những hình thức của nhận thức giác quan, và quy luật của tổng quát hóa không có gì liên hệ cụ thể với một trong hai điều này. Quy tắc thì hoàn toàn tổng quát. Hintikka giảm thiểu những luận điểm của Kant rằng những trực giác là tức thời và chúng gắn liền với nhận thức hay những hình thức của nó. Ông chỉ trích Kant vì có cái nhìn quá hạn hẹp về phạm vi của ‘trực giác’. Hầu hết những nhà bình luận không đi theo Hintikka ở đây, và cố gắng phân định một vai trò trực tiếp hơn với tính tức thời và những hình thức của nhận thức trong triết học của toán học của Kant (xem, thí dụ như Parsons 1969, và Bài viết tái bản, Parsons 1983: Tiểu luận 5). Hầu hết những học giả đều chủ trương rằng những tiên đề của hình học là tổng hợp, và do đó trạng thái của lôgích là không liên hệ.

Chúng ta hãy xem xét một đoạn văn nữa trong đó Kant giải thích rõ hơn sự khác biệt giữa toán học và phân tích khái niệm của ‘triết học’: [14]

Triết học chỉ tuân theo những khái niệm phổ quát. Toán học không thể hoàn tất được gì với chỉ đơn thuần khái niệm nhưng ngay lập tức vội vàng đến với trực giác, trong đó nó chiêm nghiệm khái niệm một cách cụ thể [15], thế nhưng không duy nghiệm; đúng hơn, toán học chiêm nghiệm chỉ khái niệm trong một trực giác vốn nó trưng bày tiên nghiệm – tức là một trực giác vốn nó đã xây dựng ... Đem cho một triết gia khái niệm của một tam giác, và để người ấy khám phá theo cách riêng của ông, liên hệ của tổng số của những góc của nó với một góc vuông có thể là gì. Bây giờ người ấy không có gì ngoài khái niệm của một hình vẽ có ba đoạn thẳng bao quanh – với hình này – và khái niệm của ba góc tương tự. Bây giờ, bất kể người ấy ngẫm nghĩ bao lâu về khái niệm này, người ấy sẽ không tìm ra được điều gì mới. Người ấy có thể mổ xẻ và phân biệt khái niệm về đường thẳng, về góc, hay về số ba, nhưng người ấy không thể đi đến bất kỳ tính chất nào khác không liên kết với những khái niệm này. Nhưng bây giờ hãy để nhà hình học giải đáp câu hỏi này. Người ấy bắt đầu ngay lập tức bằng việc xây dựng một hình tam giác. Người ấy . . . kéo dài một cạnh của tam giác này và do đó có được hai góc kề vốn cùng nhau chúng bằng hai góc vuông. . . Bây giờ người ấy chia góc bên ngoài bằng việc vẽ một đường song song với cạnh đối diện của tam giác; và người ấy thấy rằng ở đây đưa ra một góc kề bên ngoài bằng với góc bên trong; v.v ... Theo cách này, người ấy đến, bằng một chuỗi những suy luận nhưng luôn được trực giác hướng dẫn, đến một lời giải hoàn toàn hiển nhiên và đồng thời là lời giải phổ quát của vấn đề. (Critique of Pure Reason, B743-5)

Ở đây Kant nhắc đến chứng minh tiêu chuẩn theo Euclid rằng tổng số những góc trong một tam giác thì bằng hai góc vuông (180 °), thấy trong Quyển 1, Mệnh đề 32 của Elements của Euclid. Cái nhìn của Kant thì có tính gợi dẫn. Như đã nói ở trên, phân tích khái niệm không tạo kiến thức mới nhung chỉ khơi mở những gì ẩn chìm trong những khái niệm. Nó chỉ đơn thuần là ‘mổ xẻ’ hay ‘làm phân biệt’ những phần vốn đã sẵn có ở đó. Ngược lại, toán học thực sự tạo kiến thức mới. Những kết luận của nó không ẩn chìm trong những khái niệm. Trực giác đem cho cho chúng ta những thí dụ về những đối tượng hay nhóm đối tượng thể hiện những khái niệm được nói đến. Có nghĩa là, trực giác tạo ra những hình hình học hay những sưu tập được đánh số của những đối tượng. Tuy nhiên, đây chỉ là một khởi đầu sơ sài. Chỉ với những thí dụ, nhà toán học không thể đạt được nhiều hơn những gì sẽ có sẵn từ phân tích khái niệm. Cho đến giờ, tất cả những gì người ấy biết về những thí dụ là chúng có những khái niệm đã cho đang được nói đến, và như thế bất kỳ khái niệm nào khác có trong chúng. Toán học mở ra kiến thức mới qua một tiến trình tinh thần tiên nghiệm của sự xây dựng. Nhà toán học làm việc và hành động trên những thí dụ đã cho, tuân theo những quy tắc ẩn chìm trong ‘trực giác thuần túy’.

Hintikka (1967: §8) cho thấy rằng mô thức của Kant là Elements của Euclid, và là đáng vắn tắt nhìn vào cấu trúc của một chứng minh điển hình theo Euclid. Nó bắt đầu với một ‘nói rõ ra’ của một mệnh đề tổng quát, trong đó nêu lên những gì sẽ được thiết lập. Mệnh đề 32 của Sách 1 có nội dung (một phần), ‘Trong bất kỳ tam giác nào ... ba góc trong ... bằng hai góc vuông’. Sau đó, Euclid giả định rằng một hình cụ thể, thỏa mãn giả thuyết của mệnh đề, đã được vẽ ra. Điều này được gọi là ‘cắm mốc’ hay ecthesis. Với Kant, ‘cắm mốc dựng cọc’ này bao gồm trực giác, như nói trên. 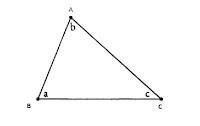Trực giác đem cho những trường hợp trừn bày những khái niệm đã cho. (Xem phần bên trái của Hình 4.1.) Phần thứ ba quan trọng của phần chứng minh là chỗ hình được xong xuôi bằng việc vẽ thêm một số đường, hình tròn, điểm, v.v. Trong thí dụ dưới đây, điều này sẽ là sự kéo dài của đoạn thẳng AB tới AD và đoạn BE song song với AC. (Xem bên phải của Hình 4.1.) [16]

Hình 4.1. Chứng minh tổng số những góc trong một tam giác bằng hai góc vuông

Có lẽ những cấu trúc phụ trợ này là bản chất của trực giác thuần túy liên quan đến toán học. Nhà hình học (trong trường hợp này là Euclid) tạo ra những sự vật không có trước đây. Sau đó, Euclid tiếp tục với chứng minh, hay apodeixis, vốn gồm một chuỗi những suy diễn liên quan đến hình đã hoàn thành. Trong thí dụ trên, chúng ta nhận thấy rằng góc ∠ CAB bằng ∠ EBD (theo định lý trước) và ∠ ACB bằng ∠ CBE. Như vậy, ba góc của tam giác cộng lại thì bằng hai góc vuông.

Trong đoạn đã dẫn, Kant nói rằng những suy luận ‘luôn luôn được trực giác hướng dẫn’. Trực giác liên quan đến việc đọc những sơ đồ và do đó mở ra cho thấy những sự kiện về hình tam giác ban đầu. Phần cuối cùng, phần ‘chứng minh’ của phần minh chứng mang lại kiến thức tổng hợp.[17]

Tiếp theo, hãy xem xét những gì Kant nói về 7 + 5 = 12. Lại nữa, phân tích về khái niệm không mang lại tổng số, vì không gì trong khái niệm của bảy và của năm cho chúng ta số mười hai. Để có tổng số, chúng ta dùng trực giác có sẵn tương ứng với một trong hai: thí dụ: năm ngón tay của chúng ta hay ... năm dấu chấm’. Điều này tương ứng với việc ‘cắm mốc’ trong một minh chứng của Euclid. Chúng ta cần một thí dụ của một sư tập của năm đối tượng. Tuy nhiên, điều này thì không đủ, vì chúng ta vẫn chưa có tổng số. Vì vậy, chúng ta ‘dần dần cộng, vào khái niệm bảy, những đơn vị của năm được cho trong trực giác’. Bước quan trọng này, nơi chúng ta tiếp tục ‘cộng’ một đơn vị, tương ứng với sự xây dựng phụ. Do đó, nhà toán học tạo ra những số 8, 9, 10, 11, và cuối cùng người ấy thấy ‘con số 12 xuất hiện’. Do đó, người ấy xây dựng một gì đó vốn không ẩn chìm trong khái niệm ban đầu của tổng số của 7 và 5, cũng không trong những thí dụ được trực giác đã cung cấp. Charles Parsons (1969) cho thấy rằng bất cứ khi nào Kant nói về chủ đề này, ông tuyên bố rằng con số, và do đó số học, liên quan đến sự kế tiếp trong một cách thức quan trọng’.

Ở đây chúng ta thấy số học giải quyết với triển vọng đi đến vô hạn trong tương lai như thế nào. Chúng ta trực giác rằng chúng ta luôn luôn có thể tiếp tục đếm.

Để chắc chắn, có một khác biệt quan trọng giữa những thí dụ hình học và số học của chúng ta. Với những tổng số đơn giản, không có gì tương ứng với ‘giai đoạn chứng minh’ của một minh chứng theo Euclid. Một xay dựng phụ hoàn thành, chúng ta có tổng số và như vậy là xong. Kant đã nêu lên rằng số học không có những tiên đề (thí dụ Critique of Pure Reason, B204--6). Điều này có thể có nghĩa là ông chủ trương rằng không có những chứng minh về số học.[18] Tuy nhiên, những tương đồng giữa số học và hình học thì rất nổi bật. Trong cả hai trường hợp, xây dựng là thiết yếu với tiến bộ toán học.

Để theo đuổi diễn giải này, hay xây dựng lại giải thích của Kant về toán học. chúng ta cần tập trung trên bản chất của xây dựng toán học. Ý tưởng là trực giác thuần túy hợp thức việc chúng ta khám phá (tiên nghiệm) những có thể có cho hoạt động về xây dựng. Những định đề Euclid phân định những xây dựng có thể có trong không gian. Thí dụ, bất kỳ đoạn thẳng nào cũng có thể được kéo dài vô hạn, hay trong lời Euclid, nhà hình học có thể tạo ra một đoạn thẳng hữu hạn liên tục trên một đường thẳng (Định đề 2). Trong số học, một nguyên tắc tương ứng là bất kỳ số nào cũng có thể được kéo dài đến số kế tiếp. Điều này được dùng trong thảo luận của 7 + 5 = 12. Theo giải thích này, những định đề cho chúng ta biết nhà toán học có thể làm gì. [19] Điều này làm toán học chủ yếu là một hoạt động trí óc, và chủ đề-nội dung của nó có thể là hoạt động tinh thần của con người (xem Parsons 1984). Chúng ta sẽ gặp lại ý tưởng của xây dựng toán học với một số dạng của thuyết trực giác – có lẽ là triết học của toán học thế kỷ XX gần nhất với Kant (xem chương 7).

Chúng ta phải thắt chặt liên kết giữa trực giác thuần túy tiên nghiệm này và nhận thức giác quan thông thường, hay trực giác duy nghiệm. Như trên, trực giác thuần túy phân định những dạng của sự nhận thức. Một giải thích là xây dựng toán học mở ra cho thấy những có thể có được của tri giác trong không gian và thời gian. Thí dụ, số học mô tả những thuộc tính của những sưu tập đã nhận thức của những đối tượng. Từ viễn tượng này, hình học thì rắc rối khó khănnhiều hơn. Về cách giải thích được nói đến, những định đề Euclid mô tả những đường có thể có vốn chúng ta có thể thấy. Tuy nhiên, nếu chúng ta nhìn xuống một đoạn dài của những đường thẳng song song, chẳng hạn như một cặp đường rầy xe điện, chúng có vẻ như gặp nhau. Nếu chúng ta xoay một vòng tròn, nó có vẻ như hình elip. Tóm lại, hình học Euclid không phải lúc nào cũng mô tả không gian hiện ra như thế nào. Tri giác thì phóng chiếu [20], không phải theo như Euclid. Vì Kant gắn trực giác với tri thức giác quan, và do đó là xuất hiện bên ngoài, ông phải giải quyết sự phân đôi thực tại–xuất hiện bên ngoài này. Có lẽ, một người theo Kant có thể bằng cách nào đó trừu tượng hóa từ những viễn tượng khác nhau của những người quan sát khác nhau, tìm những gì là phổ biến với họ. Một vấn đề thứ hai là với những ý tưởng hóa, một vấn đề chúng ta đã gặp trước đây và sẽ gặp lại. Một người thì đơn giản là không thể nhận thức một đường thẳng với không có bề rộng. Với những hình vẽ thực sự (hình dung qua ‘trực giác duy nghiệm’), hai đường thẳng, hay một tiếp tuyến với đường tròn, không gặp nhau ở một điểm duy nhất, nhưng ở một vùng nhỏ (được xác định bởi độ dày của những đường; xem Hình. 3.2.). Để giải quyết vấn đề này, Kant không có lựa chọn nào của Plato là tách thế giới hình học ra khỏi thế giới vật lý vốn chúng ta đang sống, với thế giới thứ hai chỉ là một thí dụ kém hơn và không toàn hảo của thế giới trước. Đó sẽ là một sự sa vào thuyết duy lý, và sẽ cắt đứt ràng buộc chặt chẽ với tri thức.

Kant lấy hình học để mô tả không gian, và như thế những hình Euclid là những phần của không gian. Chúng ta không thể nhìn thấy một đường Euclid, vì nó quá mỏng, nhưng dù sao nó cũng là một phần của không gian. Những đối tượng nhận thức hiện hữu trong không gian và chúng ta chỉ hiểu nhận thức trong phạm vi vốn chúng ta hiểu được không gian. Hình học nghiên cứu những dạng của nhận thức trong ý hướng rằng nó mô tả không gian vô hạn tạo điều kiện cho những đối tượng nhận thức. Không gian Euclid này là nền tảng cho nhận thức, và như thế nó đem cho những dạng của nhận thức hay nói theo thuật ngữ Kant là dạng tiên nghiệm của trực giác duy nghiệm. Cách chúng ta tìm hiểu về không gian tiên nghiệm là bằng việc thực hiện những xây dựng trong trực giác thuần túy và việc chứng minh những sự vật việc về những kết quả.

Liên quan giữa những hình vẽ hình học và những đối ứng đã vẽ của chúng là gì? Không ai có thể phủ nhận rằng những đường đã vẽ chỉ những đường gần đúng theo Euclid. Tuy nhiên, Kant nói đến những hình vẽ, và ‘trực giác duy nghiệm’ như phần của những minh chứng hình học, theo Euclid. Vậy khi đó vai trò của những hình vẽ trong minh chứng của Euclid là gì? Một giải thích, có lẽ, là những đường đã vẽ (và nắm bắt qua trực giác duy nghiệm) giúp nhà toán học trong việc tập trung trên những đường Euclid tương ứng. Những xây dựng trên những hình vẽ tương ứng với những xây dựng đã nắm bắt về tinh thần trong không gian theo Euclid. Chắc chắn Kant đã không nghĩ rằng là cần thiết để thực sự vẽ một hình vẽ trên giấy để nắm một minh chứng theo Euclid. Với một số thực hành, một người trực tiếp đi theo bản văn của một minh chứng – qua mắt nhìn của trí tưởng – không cần tham khảo sơ đồ. Tương tự, Kant chắc chắn không chủ trương rằng chúng ta phải nhìn vào một nhóm gồm năm đối tượng (chẳng hạn như ‘năm ngón tay của chúng ta hay ... năm chấm’) để tính 7 + 5. Chúng ta có thể đếm nhẩm (trong đầu). Tóm lại, những hình vẽ hay sơ đồ được vẽ trong trực giác duy nghiệm giúp đỡ não thức trong việc tập trung trên những dạng tiên nghiệm của nhận thức.

Đã đồng ý rộng rãi rằng triết học của toán học của Kant đã mất đà tiến trên những phát triển về sau trong khoa học và toán học. Thí dụ phổ thông nhất được dẫn là sự nổi lên và chấp nhận của hình học không-Euclid, và ứng dụng của nó vào vật lý. Kant đã chủ trương rằng định đề song song là một sự đúng thật tất yếu tiên nghiệm. Như thế, nó thì không thể sai, thế nhưng, theo vật lý học thời nay – một lý thuyết thực nghiệm không-thời gian thì được hiểu nhất như không-Euclid. Có sự bất đồng giữa những học giả về phần liệu Kant có thể cho phép hình học không-Euclid bất kỳ địa vị chính đáng nào không. Một số biện luận rằng ông đã hình dung chỉ một loại của tất yếu, và do đó ông có thể không phân biệt giữa hình học thuần túy và hình học ứng dụng. Nếu những học giả này đúng, khi đó với Kant hình học không-Euclid là một hình học không triển vọng. Tuy nhiên, những người khác gán cho Kant một sự phân biệt giữa khả năng về khái niệm và những gì có thể được gọi là khả năng về ‘trực giác’. Một mệnh đề, hay lý thuyết, về mặt khái niệm thì có thể có được nếu sự phân tích của những khái niệm liên quan không cho thấy một mâu thuẫn. Kant có cho phép rằng những tư tưởng nhất định vốn mâu thuẫn với hình học Euclid là mạch lạc, vì những tư tưởng đó không bao gồm một mâu thuẫn. Ông nói đến một hình mặt phẳng nằm giữa hai đường thẳng. Vì hình học Euclid là tổng hợp nên hình học không-Euclid có thể có về mặt khái niệm [21]. Tất nhiên, hình học không-Euclid thì không thể có bằng trực giác, vì hình học Euclid thì tất yếu đúng.

Về giải thích này của hình học không-Euclid, một người theo Kant sẽ phải cho phép một số học không-tiêu chuẩn có thể có về khái niệm – những gì vốn chúng ta có thể gọi là ‘số học không-Peano’. Với Kant, 7 + 5 = 12 là tổng hợp, vì vậy 7 + 5 = 10 và 7 + 5 = 13 là có thể về mặt khái niệm. Nhưng chúng ta có thể có một toán học ‘thuần túy’ mạch lạc trong đó một (hay ngay cả hai) trong những điều là đúng đúng?

Ngay cả nếu sự xoay vần khéo léo trong vấn đề đang bàn chấp nhận cho hình học không-Euclid một vài địa vị chính đáng nào đó, có lẽ như toán học thuần túy, nó không thích nghi việc dùng nó trong vật lý. Kant đã viết rằng hình học (Euclid) được hưởng ‘tính hợp lệ khách quan chỉ qua trực giác duy nghiệm, vốn ... hình thành trực giác thuần túy là của nó’. Nếu đã không vì sự liên hệ với trực giác, hình học sẽ không có tính hợp lệ khách quan gì cả, nhưng chỉ là trò chơi ... bởi sự tưởng tượng hay bởi sự hiểu biết (Critique of Pure Reason, B298). Vì hình học không-Euclid thể đoán chừng đã cắt đứt ràng buộc của Kant với trực giác, nó chỉ là trò chơi. Đến theo quan điểm của Kant khiến chúng ta biết tiên nghiệm rằng hình học không-Euclid không thể được áp dụng trong vật lý.

Có lẽ, một đáp ứng tốt hơn sẽ là cho một người theo Kant để rút lại luận điểm rằng định đề song song là tổng hợp tiên nghiệm. Trạng thái đặc biệt này được chấp thuận chỉ cho những mệnh đề vốn chúng là phổ thông với Euclid và một số hình học không-Euclid (tức là tất cả những định đề của Euclid trừ định đề thứ năm). Có lẽ nó thì không là một phần ‘cố thủ’ của triết học Kant rằng hình học theo Euclid là tổng hợp tiên nghiệm. Điều quan trọng là hình học là tổng hợp tiên nghiệm và trong thời Kant, hình học là theo Euclid. Để tránh bị lúng túng hai lần, người theo Kant của chúng ta có thể vẫn đề phòng những phát triển tương lai trong vật lý vốn phủ định một của những định đề hay tiên đề khác. Tuy nhiên, điều thắc mắc muốn biết rằng người theo Kant sẽ thay đổi quan điểm của người này về những gì có thể biết được tiên nghiệm để đáp ứng với những phát triển trong một dự án khó khăn đòi hỏi nỗ lực trí tuệ thực nghiệm như vật lý. Như chúng ta đã thấy trong chương 1, §3, một người theo thuyết duy nhiên sẽ mong đợi để sửa đổi quan điểm triết học của người này dưới ánh sáng của những phát triển của khoa học và toán học. Triết học là một dự án khó khăn đòi hỏi nỗ lực trí tuệ toàn diện. Nhưng Kant đã không là người theo thuyết duy nhiên. Ông ‘vừa vặn’ với khuôn của trường phái vốn tôi gọi là triết học-trước tiên trong chương 1, §2. Kant tự đặt mình với việc qui định những giả định-trước của kinh nghiệm và của khoa học thực nghiệm. Sự kiện rằng vật lý không tuân theo những giới hạn nghiêm ngặt thì có khó khăn sâu xa, trừ khi người theo Kant sẵn sàng để phủ nhận những phát triển trong vật lý ngoài tầm tay. Có là mạch lạc không để sửa đổi những quan điểm của một người về những gì là tiên nghiệm trong đáp ứng với khoa học thực nghiệm? Những phát triển khác trong toán học cũng chứng tỏ gây khó khăn cho những người theo Kant. Thí dụ, sự phân biệt quan trọng giữa tính liên tục và tính khác biệt và giữa đồng dạng không đổi và liên tục theo từng điểm xem dường như không có cơ sở trong trực giác. Những phân biệt này liên hệ thế nào với những hình thức của nhận thức? những nhánh khác của toán học ứng dụng và thuần túy đi xa hơn trong việc cắt đứt ràng buộc với trực giác. Chúng ta có thể liên hệ thế nào toán giải tích phức, hình học nhiều chiều, phân tích chức năng và thuyết tập hợp với những dạng của nhận thức? Nhiều những nhánh này của toán học đã tìm thấy ứng dụng trong những ngành khoa học. Thật vậy, nhiều đã được phát triển để đáp ứng với những nhu cầu của khoa học. Tất nhiên, Kant không có lỗi về điều này vì hầu hết những phát triển được nói đến xảy ra sau thời ông, nhưng ông thực đã coi những cái nhìn của ông như đem cho những giới hạn cho tất cả khoa học trong tương lai. Một người theo Kant thời nay có một khó khăn phải giải quyết.

3. Mill

Bất kể ảnh hưởng đáng kể của Kant, nhiều triết gia đã tìm thấy. và tiếp tục tìm thấy, ý niệm của ông về trực giác – và luận điểm đi kèm về sự đúng thật tiên nghiệm tổng hợp – thì khó khăn rắc rối. Theo Alberto Coffa (1991), một đề mục chính trong chương trình bàn luận của triết học trong suốt thế kỷ XIX đã là để giải thích cho tính tất yếu thoạt nhìn ban đầu và bản chất tiên nghiệm của toán học và lôgích, nhưng không phải gọi đến trực giác theo Kant. Chúng ta có thể hiểu toán học và lôgích học độc lập với những dạng của trực giác về không gian và thời gian hay không? Từ một viễn tượng thực nghiệm toàn bộ, có hai lựa chọn thay thế cho cái nhìn theo Kant, rằng toán học là tổng hợp tiên nghiệm. Người ta hoặc có thể hiểu toán học như phân tích, hoặc hiểu nó khác đi như duy nghiệm, và như thế là hậu nghiệm. Chương tiếp theo liên quan đến những nhà lôgích, những người đã theo con đường kể trước. Một số những dạng cụ thể của thuyết hình thức cũng có thể được hiểu như một bảo vệ tính phân tích của toán học [22] (xem chương 6). Bây giờ chúng ta quan tâm với một người theo thuyết duy nghiệm cấp tiến, John Stuart Mill.[23] Người đã đi theo con đường thứ hai, lập luận rằng toán học là duy nghiệm. Ông là người đi trước mở đường đối với một số những giải thích duy nghiệm về toán học, vẫn có ảnh hưởng đến thời nay (xem chương 8, §2).

Như chúng ta đã thấy, những triết gia như Kant đã tự khám phá những điều kiện tiên quyết và những giới hạn của suy nghĩ và kinh nghiệm của con người qua những phương pháp độc lập và có trước khoa học tự nhiên. Họ chủ trương rằng chúng ta cần triết học để xác định nền tảng cơ bản và những giới hạn tiên nghiệm của tất cả những điều tra thực nghiệm. Kant tự nhận mình là người tìm ra được khung cấu trúc hỗ trợ của kiến thức thực nghiệm, mà nhận thức của chúng ta phải tuân theo. Philip Kitcher (1998) gọi những quan điểm như thế này là thuyết siêu nghiệm, [24] vì chúng nhìn triết học như vượt lên trên khoa học tự nhiên. Chúng là những kiểu quan điểm vốn tôi gọi là triết học-trước tiên trong chương 1, §2, dẫn đến rằng, về mặt khái niệm, triết học xuất hiện trước mọi sự vật việc khác – chắc chắn trước khoa học theo một thứ tự nền tảng nào đó. Theo quan điểm của Kant, triết học bộc lộ những giả định-trước của khoa học thực nghiệm.

Quan điểm bây giờ gọi là thuyết duy nhiên chống lại thuyết nền tảng này [25]. Những người theo thuyết duy nhiên nhìn con người như phần hoàn toàn của trật tự nhân quả đã nghiên cứu trong khoa học. Không có nguồn kiến thức triết học nào đứng độc lập và có trước khoa học tự nhiên. Willard Van Orman Quine (1981: 72) mô tả đặc điểm thuyết duy nhiên như ‘sự từ bỏ triết học trước-tiên’ và ‘sự thừa nhận rằng nó nằm trong chính khoa học ... rằng thực tại phải được nhận biết và mô tả’ (xem thêm Quine 1969). Bất kỳ khả năng về tri thức học nào vốn triết gia dẫn nhắc phải có thể chịu được sự xem xét kỹ lưỡng thông thường và khoa học. Tri thức học hòa lẫn vào trong tâm lý học nhận thức. [26]

Mill là một trong những người theo thuyết duy nhiên nhất quán nhất trong lịch sử triết học. Chống lại những người theo Kant, ông chủ trương rằng não thức con người hoàn toàn là một phần của tự nhiên, và do đó, không có kiến thức quan trọng nào về thế giới có thể là tiên nghiệm. Ông đã phát triển một tri thức học trên cơ sở duy nghiệm triệt để đó.

Phân biệt của Mill giữa những mệnh đề “nói” và “thực” xem dường như đã mô phỏng theo sự phân đôi phân tích-tổng hợp của Kant, hay đúng hơn là sự phân biệt của Hume giữa “những liên hệ của những ý tưởng” và “những vấn đề của thực tế”. Đối với Mill, những mệnh đề nói ra bằng lời đều đúng bởi định nghĩa. Chúng không có nội dung ban đầu và không nói bất cứ gì về thế giới. Mill khác với Kant và một số người theo thuyết duy nghiệm khác, chẳng hạn như Hume trước ông và Rudolf Carnap [27]sau ông, trong chủ trương rằng những mệnh đề của toán học – và hầu hết của lôgích – là thực và do đó tổng hợp và duy nghiệm. Trong thuật ngữ của Hume, toán học và lôgích với Mill là về những vấn đề thực tế.

Không giống như những người theo thuyết duy nghiệm trước đó và sau này, suy luận cơ bản về tri thức học của Mill là quy nạp liệt kê. [28] Chúng ta thấy nhiều những con quạ đen và không thấy con nào có bất kỳ màu nào khác, và kết luận rằng tất cả những con quạ đều màu đen, và rằng con quạ lần sau chúng ta nhìn thấy sẽ là màu đen. Tất cả kiến thức (thực) về thế giới đều gián tiếp bắt nguồn từ những khái quát hóa trên quan sát. Tri thức học toàn diện của Mill thì tinh vi phức tạp, và gồm những nguyên tắc nổi tiếng của ông về nghiên cứu thực nghiệm trong khoa học. Liên hệ về tri thức giữa những quy luật khoa học và những khái quát hóa từ kinh nghiệm thì đúng hơn là đi đường vòng, không trực tiếp. Tuy nhiên, tri thức học cho toán học và lôgích học của Mill thì không phức tạp như thế. Ông chủ trương rằng những quy luật toán học và lôgích có thể được truy nguồn trực tiếp đến suy luận quy nạp liệt kê – những suy luận từ sự quan sát qua những khái quát hóa trên những gì đã quan sát.

Ở ít nhất một chỗ, Mill đề nghị rằng những khái quát hóa không công gì thêm cho sức mạnh của những lập luận, vì tất cả những suy luận quan trọng đều từ ‘những cá biệt đến những cá biệt’. Những mệnh đề phổ quát, như ‘tất cả những con quạ đều màu đen’, chỉ là những ‘ghi chép’ kết luận tóm tắt của những gì chúng ta đã quan sát được và những gì chúng ta mong đợi sẽ quan sát được. Với Mill, những mệnh đề toán học điển hình là những khái quát hóa, và vì vậy những mệnh đề này cũng ghi chép và kết luận tóm tắt kinh nghiệm. Triết học của toán học của Mill được thiết kế để cho thấy những mệnh đề toán học là gì, để đem chúng vào phù hợp với chủ đề tri thức học tổng quát này.

Chúng ta hãy bắt đầu với hình học. Mill bác bỏ sự hiện hữu của những đối tượng trừu tượng, và ông tìm để xây dựng hình học trên sự quan sát. Như thế, giống Aristotle, ông phải giải thích cho ý hướng hiển nhiên trong đó những đối tượng nghiên cứu trong hình học thì không giống như bất cứ gì chúng ta quan sát trong thế giới vật lý. Mọi đường thẳng chúng ta thấy đều có bề rộng và không hoàn toàn thẳng. Bài viết của Mill về vấn đề này không rõ ràng, nhưng có thể đưa ra một tóm lược tổng quát. Ông chủ trương rằng những đối tượng hình học là những gần đúng của những hình dạng thực sự. Hình học là về những ý tưởng hóa của những có thể có của xây dựng. Hai khái niệm trung tâm ở đây là ‘ý tưởng hóa’ và ‘tính có thể có’. Người theo thuyết duy nghiệm kiên quyết này hiểu thế nào những khái niệm này?

Mill lấy những đường không rộng và những điểm không dài để là những khái niệm giới hạn. Cho một đường kẻ trên giấy có thể là đậm nhạt ít nhiều, tùy phẩm chất của mực, độ sắc nét của bút chì hay độ phân giải của máy in. Chúng ta có thể nghĩ những đường hình học như giới hạn tiến đến gần khi chúng ta vẽ những đường có nét càng nhỏ hơn, và những đường thẳng càng thẳng hơn. Tương tự, một điểm là giới hạn tiến đến gần khi chúng ta vẽ những đoạn thẳng sắc nét hơn và ngắn hơn, và một đường tròn là giới hạn tiến đến gần khi chúng ta vẽ những đường tròn mỏng hơn và toàn hảo hơn. [29] Về vật lý, tất nhiên, không có những giới hạn loại giống vậy và Mill đã chủ trương rằng hình học không giải quyết với những đối tượng đang hiện hữu. Vì vậy, nói cho đúng theo Mill, hình học Euclid là một công trình của tưởng tượng. Những hình dạng đã công nhận (qua định đề) là những ‘đại diện giả tạo’. Tuy nhiên, vì những hình dạng hình học gần đúng với những hình đã vẽ và với những đối tượng tự nhiên, những mệnh đề hình học là đúng (về tự nhiên) đến mức độ vốn những hình dạng thực và những đối tượng gần đúng với những ý tưởng hóa. Nếu chúng ta đo những góc của một tam giác đã vẽ, chúng ta sẽ thấy tổng số là khoảng hai góc vuông. Những đường thẳng vẽ tam giác càng thẳng và càng sắc nét thì những góc của chúng càng gần hơn để bằng hai góc vuông. Nếu chúng ta kỹ lưỡng vẽ một tam giác, chúng ta sẽ thấy rằng ba đường trung tuyến thẳng góc (với mỗi cạnh) cắt lẫn nhau. Nếu chúng ta cẩu thả (nhưng không quá cẩu thả), chúng ta sẽ thấy rằng những đường trung tuyến gần như cắt lẫn nhau (ở một điểm) [30]. Trong ý hướng này, những mệnh đề của hình học là những khái quát quy nạp về những hình dạng vật lý có thể có trong không gian vật lý. Chúng đã được kinh nghiệm lâu đời xác định.

Người ta có thể biện luận ý niệm cuả tính có thể có (khả năng) vốn Mill gọi đến trong giải thích về hình học của ông. Để tập trung trên một thí dụ, chúng ta hiểu thế nào về định đề Euclid rằng giữa hai điểm bất kỳ người ta có thể vẽ một đường thẳng? Nếu điều này có nghĩa là chúng ta có thể vẽ một đường thẳng không bề rộng, khi đó định đề này thì không đúng ngay cả với xấp xỉ gần đúng. Thật vậy, chúng ta không thể mường tượng được ngay cả việc vẽ một đường không bề rộng. Chúng ta sẽ dùng dụng cụ nào? Bàn về những giới hạn đề nghị rằng định đề có thể có nghĩa là nếu chúng ta được cho bất kỳ hai điểm vật lý A, B, bất kể nhỏ đến mức nào, và nếu chúng ta được cho bất kỳ độ dày d nào, chúng ta có thể vẽ một đường thẳng giữa A và B không dày (đậm nét) hơn d. Điều này thì không tốt hơn gì nhiều, vì chúng ta không thể xem phát biểu-giới hạn này như một sự tổng quát hóa đã thiết lập vững chắc từ kinh nghiệm. Chúng ta đã có được bao nhiêu kinh nghiệm với những đường kẻ vẽ thật mỏng? Ngay cả có phải sự khái quát thì đúng không? Như đến giờ chúng ta biết, có một giới hạn thấp hơn với độ dày của một đường vốn chúng ta có thể vẽ và nhận biết. Chúng ta có thể vẽ một đường mỏng hơn đường kính của một atom hydro không? Bằng chất liệu gì? Được hiểu theo những thuật ngữ vật lý rõ ràng như vậy, dạng cụ thể giới hạn của định đề Euclid chắc chắn thì sai. Tương tự, định lý rằng mọi đường thẳng đều có một đường trung tuyến vuông góc thì sai về mặt vật lý, ngay cả cho phép những ý tưởng hóa của Mill. Giả định chúng ta bắt đầu với một đoạn thẳng cho trước, dài hai cm, và chia đôi nó. Sau đó chia đôi nửa bên trái, rồi chia đôi nửa bên trái đó, tiếp tục càng lâu càng tốt. Đơn giản là không thể nào tiếp tục điều này ba mươi lần. Đoạn thẳng thứ ba mươi sẽ có một độ dài dưới-atom.

Vậy có thể vẽ một đoạn thẳng giữa hai điểm, hay cắt thành hai phần bằng nhau một đoạn thẳng bất kỳ theo nghĩa nào? Có lẽ Mill đã lấy hình học để nói về một kinh nghiệm được cải thiện theo giả thuyết, trong đó khả năng nhạy bén của chúng ta là hết sức sắc bén. Hay có lẽ một người theo thuyết Mill có thể giải thích những tiên đề hình học trong những điều kiện của một khả năng toán học đặc biệt nào đó, thay vì khả năng vật lý đã dẫn nhắc ở trên. Luận điểm cơ bản là nó phù hợp với những luật toán học của không gian, nếu không nói những luật vật lý của vũ trụ, rằng không có giới hạn về độ mỏng của những đường thẳng và không có giới hạn với những đoạn thẳng có thể cắt được thành hai phần bằng nhau. Tuy nhiên, thật khó để thấy Mill có cung ứng nào để tạo ra hoặc khả năng giả định hết sức nhạy bén đã cải thiện, hoặc những khả năng toán học đặc biệt. Hãy nhớ rằng, với Mill, tất cả kiến thức toán học đều dựa trên những khái quát hóa quy nạp từ kinh nghiệm. Vậy chúng ta sẽ học ở đâu về những khả năng hết sức nhạy bén và những khả năng toán học?

Bây giờ chuyển sang số học, Mill đồng ý với Plato và Aristotle rằng số tự nhiên là những con số của những sưu tập. Ông đứng về phía Aristotle trong việc phủ nhận những ‘đơn vị’ lý tưởng và vì vậy, với Mill, những số là những số của những đối tượng thông thường:

Tất cả những số phải là những số của một gì đó: không có những sự vật việc như những số trong trừu tượng. Mười phải có nghĩa là mười vật thể, hay mười âm thanh, hay mười nhịp đập của mạch máu. Nhưng mặc dù những số phải là những số của một gì đó, chúng có thể là những số của sự vật việc bất kỳ nào. Do đó, những mệnh đề liên quan đến những số, có một điểm khác thường đáng chú ý là chúng là những mệnh đề liên quan đến tất cả sự vật việc dù là gì, tất cả những đối tượng, tất cả những hiện hữu thuộc mọi loại, biết được với kinh nghiệm của chúng ta. (Mill 1973: 254-5)

Do đó Mill không coi một chữ số là một riêng lẻ/cụ thể vốn biểu thị một đối tượng độc nhất. Đúng hơn, những chữ số là những thuật ngữ tổng quát, như ‘con chó’ hay ‘màu đỏ’. Chúng không gồm những đối tượng riêng lẻ, nhưng gồm những kết tập của những đối tượng: Thí dụ, ‘hai, biểu thị tất cả những cặp/đôi của sự vật việc, và mười hai cho tất cả những tá của sự vật việc’ (1973: 610).

Những mệnh đề số học là gì? Mill quan tâm với việc đưa ra một giải thích của những tổng số, như ‘5 + 2 = 7’ và ‘165 + 432 = 597’. Ông nói rằng chỉ có hai tiên đề, đó là ‘những sự vật việc vốn đều bằng với cùng những sự vật việc đều bằng với lẫn nhau’ và ‘những bằng nhau cộng với những bằng nhau tạo những tổng số bằng nhau’ (1973: 610) và một giản đồ định nghĩa, một cho mỗi chữ số biểu thị con số được ‘hình thành’ bằng cộng thêm một đơn vị vào số ngay bên dưới nó. Từ điều này, ông đưa ra một diễn dịch của ‘5 + 2 = 7’. Là rõ ràng để mở rộng cách tiến hành để lấy được bất kỳ tổng số chính xác nào như thế nào.[31]

Đặc điểm nổi bật ở đây, với Mill, là rằng những tổng số này là những mệnh đề thực, không phải lời nói về những kết tập vật lý và những thuộc tính cấu trúc của chúng. Vì chúng là thực, cuối cùng chúng phải được biết bằng quy nạp liệt kê, sự khái quát hóa trên kinh nghiệm. Kinh nghiệm hầu như đồng nhất của chúng ta với việc thu thập và phân tách những đối tượng xác nhận những tổng số số học. Trong một đoạn văn nhiều tai tiếng, Mill đã viết rằng tổng số ‘2 + 1 = 3’ gồm giả định ‘rằng những sưu tập của những đối tượng hiện hữu, vốn trong khi chúng gây ấn tượng giác quan, cách này 0 ⁰ 0, có thể được phân tách vào thành hai phần, cách này, 00 0’ (1973: 257).

Foundations of Arithmetic của Frege gồm một tấn công dai dẳng và chua chát trên giải thích của Mill về số học:

Thật là may mắn, sau đó, rằng không phải mọi sự vật việc trong thế giới thì được xác định chặt chẽ; vì nếu đã thế, chúng ta sẽ không có khả năng để làm được sự phân tách này, và ‘2 + 1 sẽ không là 3’ Thật may mắn là Mill cũng đã không minh họa những sự kiện vật lý cơ bản cho những số zero và 1 ! ... Từ điều này, chúng ta có thể thấy rằng thực sự là không chính xác để nói về ba tiếng gõ khi đồng hồ điểm ba, hay gọi ngọt, chua và đắng là ba cảm giác . Vì không một nào của những điều này tao ấn tượng giác quan, cách này 0 ⁰ 0’. (Frege 1884: §7)

Do đó, Frege lấy bài nói về việc sắp xếp của Mill trong một nghĩa vật lý thẳng thừng: ‘Chúng ta có phải tổ chức, theo đúng nghĩa đen, một đại hội của tất cả người mù ở Germany trước khi chúng ta có thể gắn bất kỳ ý nghĩa nào với cụm từ diễn đạt “số những người mù ở Germany”?’ (§23).

Phê bình của Frege thì không công bằng. Như chúng ta đã thấy ở trên, tự thân Mill nói về số của những sự vật việc vốn không thể được sắp xếp trong cụ thể vật chất vào những đỉnh của một tam giác. Ông nói về những tiếng động và những nhịp tim đập. Như thế, Mill phải có một gì tổng quát hơn trong não thức. Gom góp và tách biệt những sưu tập nhỏ gồm những đối tượng là một trường hợp thí dụ điển hình của sự tổng quát hóa những tổng số trong số học. Chúng ta thực hiện việc thu thập và tách biệt nhịp tim và chuông đồng hồ trong não thức, chưa kể đến những lục địa và những hành tinh, ngay cả nếu chúng không gây ấn tượng giác quan, cách này 0 ⁰ 0, và không thể tách biệt về vật lý, cách này 00 0’. Chúng ta cũng thu thập một hay ngay cả zero đối tượng của một loại nhất định, khi chúng ta xem xét có bao nhiêu quân vua trắng trên một bàn cờ chess, hay bao nhiêu nữ tổng thống US đã nhậm chức trước năm 1999.

Tuy nhiên, Frege thì đúng rằng gánh nặng nghiêm trọng với người theo thuyết duy nghiệm là để hiểu ý nghĩa mạch lạc và rõ ràng của những thuật ngữ ‘thu thập’ và ‘phân tách’. Chính xác kinh nghiệm nào thì gồm trong việc nêu lên rằng hai nhịp tim đập cộng với một nhịp tim tạo ra ba nhịp tim đập, hay hai hành tinh cộng với ba hành tinh thành năm hành tinh?

Frege cũng đặt câu hỏi về ý tưởng của Mill rằng những con số biểu thị những kết tập vật chất. Nếu chúng ta nghĩ về một kết tập như một ‘đụn-đống’ của lỉnh kỉnh chất liệu vật chất, chúng ta sẽ không thể gán kèm một con số vào nó: Nếu tôi đặt một xấp quân bài vào tay [ai đó], với lời bảo: Tìm con số cúa xấp này, điều này không bảo người ấy rõ liệu tôi muốn biết con số của những quân bài trong xấp, hay của bộ bài đầy đủ những quân bài, hay ngay cả nói về điểm trong một ván bài Skat. Đưa cho người ấy cái xấp bài vào tay chưa phải là đã trao cho người ấy hoàn toàn đối tượng vốn người ấy sẽ điều tra; Tôi phải thêm một số từ khác – quân bài, hay bộ bài, hay điểm. (1884: §22). Trong phần tiếp theo, Frege đã viết rằng ‘một bó rơm có thể được tách thành nhiều phần bằng việc cắt đôi tất cả những cọng rơm, hay bằng việc tách nó thành những cọng rơm đơn lẻ, hay bằng việc chia nó vào thành hai bó’. Ông thêm rằng ‘từ số “một” ... trong cụm từ “một cọng rơm” là dấu hiệu của thất bại, không đúng với cách thức trong đó cọng rơm được tạo thành từ những tế bào hay phân tử’

Tự thân Mill (1973: 611) đã trả lời Frege ở đây: ‘Khi chúng ta gọi một sưu tâp của những đối tượng là hai, ba hay bốn, chúng không là hai, ba hay bốn trong trừu tượng; chúng là hai, ba, hay bốn của những sự vật việc thuộc của một loại nhất định nào đó; những hòn sỏi, những con ngựa, những inches/thước đo, những pound/kg nặng. Những gì là tên gọi của con số có nghĩa là cách thức trong đó những đối tượng đơn lẻ của loại đã cho phải được đặt vào cùng nhau, để tạo ra kết tập (gói/bó đống/đụn) cụ thể đó’. Khi đó, với Mill, một kết tập thì đông nhất với khối vật của những lỉnh kỉnh này nọ cùng với những đơn vị trong đó sẽ được phân chia (và do đó được tính/đếm). Một bộ bài thì không cùng là một kết tập vật lý như 52 lá bài riêng lẻ, bốn cách xếp bài, v.v. Những kết tập nằm ở cùng một nơi vào cùng một thời điểm, nhưng dù sao chúng là những kết tập khác biệt. Tương tự như vậy. kết tập bó rơm của Frege không giống như kết tập của nửa bó rơm, hay bó của hai nửa bó, hay bó của những phân tử. Mặc dù Mill bác bỏ sự hiện hữu của những đối tượng trừu tượng, và như thế chủ trương rằng những kết tập (gói/bó đống/đụn) là vật chất, bản thể học của ông không nghiêm khắc như người ta nghĩ.

Tuy nhiên, lại nữa, gánh nặng thì trên người theo thuyết duy nghiệm để đưa ra phạm trù bản thể học này và cho thấy nó đặt nền tảng trên kinh nghiệm như thế nào. Penelope Maddy (1990: ch. 2, §2) nêu lên rằng có một sự khác biệt giữa nhìn, nói, bốn chiếc giày, và xem chúng như hai đôi. Có lẽ một gì đó giống điều này sẽ giúp người theo Mill ở đây (xem thêm Burge 1977).

Frege cũng đưa Mill đến công việc liên quan với những con số lớn. Chúng ta có kinh nghiệm về một kết tập có kích thước 1.234.457.890 hay không, và chúng ta có thể phân biệt nó với một kết tập có kích thước 1.234.457.891 hay không? Kinh nghiệm đã tổng quát hóa bởi 1.234.457.890 + 6.792 = 1.234.464.682 là gì? Chúng ta có thể mở rộng quan điểm của Frege, bằng việc hỏi chúng ta xác nhận tổng số trung bình, như 1,256 + 2,781 = 4,037 như thế nào. Giả định chúng ta lấy một mẫu ngẫu nhiên của những người lớn và đưa cho mỗi người một đống 1.256 hòn bi và một đống 2.781 hòn bi và bảo người ấy gom hai đống vào thành một đống lớn và xác định số lượng của nó. Sự chú ý của con người là những gì như nó vẫn là, rất ít (nếu có) của những đối tượng của chúng ta sẽ cho ra con số cuối cùng là 4.037. Theo cái nhìn của Mill, chúng ta có phải coi kết quả này như một sự phủ nhận tổng số không? Giả thử chúng ta dùng những con thỏ thay vì những hòn bi, và phải mất mấy tháng để làm xong thí nghiệm? Giả thử chúng ta dùng gallon của hai chất lỏng, trong đó một phản ứng hóa học hay bay hơi có thể làm thay đổi thể tích của tổng hợp? Chúng ta sẽ không có được kết quả chính xác và sẽ phải tuyên bố rằng tổng số thì không được xác nhận. Thoạt đầu, mới thoáng nhìn, có vẻ vô lý ngay cả khi thử làm thí nghiệm này để xác nhận những tổng số số học. Chúng ta biết tổng số đúng là bao nhiêu trước khi bắt đầu thí nghiệm. Chúng ta có thể dùng kết quả để xác định khả năng của những đối tượng trong việc cộng và đếm.

Theo những dòng tương tự, Mill chủ trương rằng mỗi chữ số đại diện cho những sưu tập kích thước của những con số tương ứng. Điều này dẫn đến rằng có, hay có thể có vô hạn của những đối tượng. Chúng ta có hỗ trợ thực nghiệm cho điều này không? Điều gì sẽ xảy ra nếu chúng ta áp dụng một lý thuyết vật lý vốn dẫn đến rằng chỉ có hữu hạn gồm nhiều những đối tượng vật lý. Điều này có phủ nhận số học không?

Tình trạng ở đây tương tự như sự không ăn khớp giữa những mệnh đề hình học và những phát biểu về những vật thể thông thường. Kinh nghiệm hạn chế của chúng ta không hoàn toàn ăn khớp với những mệnh đề toán học. Về hình học, một người theo Mill có thể trả lời bằng việc nói về sự ý tưởng hóa, sự có thể có, và sự gần đúng. Những mệnh đề toán học – đặc biệt là những định nghĩa của những con số – không hoàn toàn tương ứng với kinh nghiệm. Họ quan tâm với kinh nghiệm có thể có, trong những điều kiện lý tưởng trong đó khoảng kéo dài của chú ý của chúng ta được cải thiện và bất kỳ khác biệt và tác động hỗ tương nào giữa những đơn vị (có thể thay đổi số lượng theo thời gian) đều bị bỏ qua. Kinh nghiệm khẳng định rằng những mệnh đề số học là gần đúng của kinh nghiệm. Tuy nhiên, lại nữa, người theo Mill lại có gánh nặng là phải đưa ra ý tưởng về sự có thể có này.

Một chiều khác của cái nhìn của Mill, ẩn chìm trong những gì chúng ta đã thấy rồi, là ông đã rời xa đáng kể với cái nhìn đã nhận của toán học như rất (nếu không là hoàn toàn) chắc chắn và tất yếu. Theo như Mill, ngay cả nhiều mệnh đề toán học còn không đúng gì cả, chưa nói đến đúng tất yếu và không thể nghi ngờ, và chưa nói đến có thể biết được tiên nghiệm. Mill coi trọng vấn đề của việc cho thấy tại sao cái nhìn đã nhận thì thuyết phục đến vậy. Ông đặt câu hỏi: Tại sao sự chắc chắn trong toán học, và bằng chứng của minh chứng, những cụm từ phổ thông để diễn đạt mức độ cao nhất của sự bảo đảm lý trí có thể đạt được? Tại sao toán học bởi hầu hết tất cả những triết gia ... đã coi là độc lập với bằng chứng của kinh nghiệm và quan sát, và được đặc trưng như hệ thống Sự Đúng thật Tất yếu? (Mill 1973: 224). Mill chủ trương rằng số học có vẻ là tất yếu và có thể biết tiên nghiệm vì những tiên đề và những định nghĩa ‘được biết với chúng ta bởi kinh nghiệm sớm có và liên tục’ (1973: 256). Những đúng thật cơ bản của số học, chẳng hạn như những tổng số đơn giản, đã được xác nhận từ khi chúng ta bắt đầu tiếp xúc với thế giới. Điều này không làm cho chúng gốc rễ thực sự thành tiên nghiệm. Mill đồng ý rằng những tổng số số học đơn giản thí tất yếu, nhưng chỉ với nghĩa là chúng ta không thể tưởng tượng mọi sự vật việc trở nên là khác biệt (mặc dù những ý tưởng hóa đã nói ở trên). Vì vậy, thí dụ, chúng ta không thể tưởng tượng rằng một sưu tập của những những đối tượng hiện hữu, trong khi chúng gây ấn tượng với những giác quan, cách này 0 ⁰ 0, có thể được tách thành hai phần, cách này 00 0, hay ít nhất với không không thay đổi những đối tượng trong cách nào đó [32]

Mill đồng ý với những người theo Kant rằng nguồn gốc cuối cùng của tin tưởng vào những tiên đề của số học và hình học nằm trong những giới hạn của những gì chúng ta có thể nhận thức được. Những tiên đề của những lý thuyết toán học đều được lựa chọn bởi sự phản ảnh trên cách chúng ta nhận thức cấu trúc của thế giới. Tất nhiên, Mill đồng ý rằng những hiểu biết sâu xa này trong trực giác tri giác này là đáng tin cậy, ở chỗ chúng ta không bị dẫn đi lạc khi đi theo chúng và giả định, chẳng hạn, thế giới là như Euclid và rằng những kết tập đó thuận hợp với số học. Nhưng ông nhấn mạnh rằng độ tin cậy của trực giác tri giác liên quan đến những thuộc tính hình học và số học thực sự của những đối tượng vật lý là một vấn đề thực nghiệm. Đó là, chúng ta tìm ra được qua kinh nghiệm rằng trực giác tri giác là đáng tin cậy. Bằng tự quan sát, chúng ta thấy rằng chúng ta không thể nhận thức thế giới trong bất kỳ cách nào khác và sự quan sát đó tiếp tục thuận hợp với những hình thức số học và hình dạng Euclid.

Với cơ sở tri thức học nghèo nàn của quy nạp liệt kê, thật đáng chú ý rằng Mill đưa thuyết duy nghiệm kiên quyết của ông đến xa như ông làm, sau khi trình bày những giải thích triết học tinh vi về hình học và số học cơ bản Euclid. Tuy nhiên, triết học của toán học của ông không đi xa lắm. Mill chỉ nói đến hình học. số học, và một vài đại số, không là những nhánh của toán học cao cấp. Thiếu sót này có thể hiểu được ở Aristotle, tất nhiên, nhưng không dễ dàng như vậy ở đây, với sự quan trọng của toán học cao cấp trong những ngành khoa học đang phát triển vào thời của Mill.

Ngay cả những giải thích của Mill về số học và hình học cũng hạn chế nghiêm trọng trong phạm vi của chúng. Triết học số học của ông nắm bắt được nhiều hơn một chút những tổng số và những khác biệt đơn giản, những gì được học ở trường tiểu học. Nguyên lý (có lẽ không khéo gọi tên) của toán học quy nạp là luận điểm chủ trương rằng với bất kỳ thuộc tính P nào, nếu P đúng với 0, và nếu, với mọi số tự nhiên n, nếu P giữ đúng với n thì P giữ đúng với n + 1, thì P giữ đúng với mọi số tự nhiên. Trong những ký hiệu:

(P0 & ∀ x ((Nx & Px) → Px + 1)) → ∀ x (Nx →Px).

Nguyên lý quy nạp toán học là một chủ đề trung tâm của số học tiên đề. Là khó khăn để làm sáng rõ thêm về những số tự nhiên nếu không có nguyên lý này. Theo như tôi có thể nói, quy nạp liệt kê – những tổng quát hóa từ kinh nghiệm – không đem lại hỗ trợ cho quy nạp toán học. ‘Kinh nghiệm sớm có và không đổi’ nào xác nhận quy nạp toán học? Mill có thể đáp ứng rằng chúng ta không thể tưởng tượng quy nạp toán học thì sai, và ông có nhắc đến tính tin cậy thực nghiệm của khả năng của tưởng tượng này. Tuy nhiên, khó khan để thấy quy nạp toán học liên hệ trực tiếp thế nào trên kinh nghiệm. Nó mô tả những loại kinh nghiệm nào?

Ở điểm này, người theo thuyết Mill của chúng ta có thể thử dùng những động tác khéo léo theo Euclid của việc thành lập số học trên hình học (mặc dù việc này sẽ làm giảm giá trị tính ứng dụng phổ quát của số học). Một tương tự hình học của quy nạp toán học là nguyên lý Archimede, rằng với hai đoạn thẳng a, b bất kỳ, có một số tự nhiên n, sao cho nhân n-lần của a thì dài hơn b. Một người theo Mill có thể cho thấy rằng nguyên lý này được xác nhận bởi kinh nghiệm sớm có và không đổi (miễn là chúng ta nói về khả năng toán học nhưng không phải khả năng vật lý). Một thí dụ ngược lại với nguyên tắc Archimede sẽ là một cặp của đoạn thẳng, một đoạn thẳng thì ngắn hơn, gần đến vô hạn, so với đoạn thẳng kia. Chắc chắn, chúng ta không có kinh nghiệm trực tiếp nào về những vô hạn, ngay cả khi chúng ta gắng tưởng tượng chúng. Ngay cả nếu người theo Mill của chúng ta có thể liên hệ nguyên lý quy nạp toán học với nguyên lý Archimede, thì điều này cũng không giúp được gì nhiều để thành công. Tiên đề bao hàm [33] sẽ là một trở ngại thêm nữa. Trong giải tích thực, nguyên lý phát biểu rằng mọi set gồm những số thực có giới hạn đều có một giới hạn trên nhỏ nhất. Một tương tự trong hình học là thuộc tính Bolzano-Weierstrass rằng mọi set vô hạn, có giới hạn có một điểm giới hạn. Vì chúng ta không có kinh nghiệm với những set vô hạn của những điểm hay những đối tượng, nên xem dường như không có cơ sở cho những những nguyên lý này trong quy nạp liệt kê.

Chúng ta hãy xem xét lại trước khi kết luận. Chúng ta đã ghi nhận một số phê bình cứng rắn về những ý niệm khác nhau của ‘khả năng’ cần thiết để duy trì giải thích của Mill về toán học. Mặc dù những điều này có thể được khắc phục, nhưng có vẻ rằng gánh nặng phản bác là một khó khăn. Thứ hai, và quan trọng hơn, quyết định của Mill để dựa tất cả toán học và lôgích dựa trên quy nạp liệt kê thì không thể được duy trì được. Vì những lý do giống như của những đã nêu ở đây, những người theo thuyết duy nghiệm đương thời không cố gắng bảo vệ Mill về những vấn đề này. Tuy nhiên, động lực chính của thuyết duy nghiệm của Mill vẫn sống đến ngày nay, và có lẽ còn mạnh. Một nhóm cốt lõi gồm những triết gia tận tụy chấp nhận và bảo vệ ‘phương diện cấp tiến’ của thuyết duy nghiệm của Mill, quan điểm chủ trương rằng lôgích và toán học chứa những định đề ‘tổng hợp’ hay ‘thực’, và trái ngược với Kant, rằng những định đề này được biết đến hậu nghiệm, cuối cùng theo kinh nghiệm.

Kitcher (1983, 1998) đem cho một giải thích tinh tế và phức tạp về toán học cao cấp trong một khung cấu trúc hỗ trợ gần như theo Mill. Giống Mill, Kitcher đem toán học đến liên quan với những khả năng của con người để xây dựng và thu thập, nhưng ông nói rõ hơn Mill về những ý tưởng hóa liên quan. Thay vì nói về những hoạt động thu thập và xây dựng của con người thực sự, Kitcher nói về hoạt động của những người xây dựng lý tưởng tưởng tượng, những người không có cùng những giới hạn của con người về thời gian, không gian, khoảng thời gian chú ý, hay ngay cả đời sống. Những người xây dựng lý tưởng vẽ những đường không bề rộng và họ thu thập những kết tập lớn. Thí dụ, những tiên đề về quy nạp toán học và thuộc tính BalzanoWeierstrass trình bày những phát biểu về những khả năng được phân phát cho những người xây dựng lý tưởng, tương ứng với số học và giải tích thực. Những người xây dựng lý tưởng này giải quyết những set vô hạn của những đoạn thẳng và lấy những điểm giới hạn và giới hạn trên của chúng. Với Kitcher, đúng thật toán học – những mệnh đề về những người xây dựng lý tưởng – liên quan đến những đúng thật về những khả năng của con người sự lý tưởng hóa và tính gần đúng vốn ít nhiều không phức tạp. Trong những ngành cao cấp hơn, chẳng hạn như thuyết tập hợp, những ý tưởng hóa thực sự rất lý tưởng. Cho mỗi số đếm vô hạn K, người xây dựng lý tưởng có thể tạo ra một sưu tâph có kích thước K. Tuy nhiên, liên hệ với sự xây dựng con người thực tế thì không bị bỏ quên.

Tất nhiên, không như Mill, Kitcher không chỉ dựa trên quy nạp liệt kê để đặt nền tảng cho toán học và lôgích. Những chuyển dịch được phân phát cho người xây dựng lý tưởng thì chính đáng trên cơ bản của sự hữu dụng của lý thuyết trong tổng thể nỗ lực hoạt động khoa học . Kitcher vẫn là một người duy nghiệm cấp tiến, trong đó mục tiêu bao trùm của toàn bộ nỗ lực hoạt động khoa học – toán học – là để giải thích cho kinh nghiệm. Ông cùng với Mill bác bỏ quan điểm đã nhận rằng toán học là biết được tiên nghiệm. Kitcher lập luận rằng chúng ta cần kinh nghiệm để xác định đúng những ý tưởng hóa nào là có ích trong việc đoán trước kinh nghiệm và kiểm soát môi trường. Toán học thì không thể sửa đổi, vì chúng ta phải không đóng lại những khả năng của những ý tưởng hóa hoàn toàn khác nhau, và do đó, toán học khác biệt hoàn toàn. Trong chương 8, §2 dưới đây, chúng ta xem xét một người theo thuyết duy nghiệm kiên quyết khác, Quine, người duy trì một tri thức học diễn dịch-giả thuyết cho tất cả toán học và khoa học, nhưng lại khác xa Mill ở chỗ không coi toán học là về hoạt động xây dựng thực hay lý tưởng. Trong thời gian đó, chúng ta chuyển sang những cái nhìn khác về toán học, gồm một thuyết duy nghiệm ít triệt để hơn (chương 5, §3).

4. Đọc thêm

Xem Coffa 1991: ch. 1, và những tài liệu trong Posy 1992 cho một bắt đầu rất tốt trên sự giàu có của nghiên cứu hàn lâm trên triết học của Kant về toán học (đặc biệt là bài giới thiệu của Posy). Tuyển tập chứa những tài liệu đã trích dẫn ở trên Parsons 1969, 1984, Friedman 1985, Hintikka 1967, và Posy 1984, cũng như rất nhiều những công trình có ảnh hưởng và thể hiện sự hiểu biết chính xác và sâu sắc khác. Cũng xem thêm Friedman 1992. A System of Lôgic (1973) của riêng Mill là một giải thích dễ đọc về những quan điểm về toán học của ông. Nguồn thứ cấp chắc chắn là Skorupski 1989: ch. 5. Cũng xem thêm những tài liệu trong Skorupski 1998, đặc biệt là Skorupski 1998a và Kitcher 1998.

Lê Dọn Bàn tạm dịch – bản nháp thứ nhất

(Jan/2022)

(Còn tiếp... →)

http://chuyendaudau.blogspot.com/

http://chuyendaudau.wordpress.com

[1] [Không phải là không phổ thông khi những chuỗi trong lịch sử triết học nhảy từ Aristotle sang cái gọi là thời kỳ thời nay (‘hiện đại’, với Bacon hay Hobbes, hay ngay cả là Descartes. những khóa học trong lịch sử toán học thường có một khoảng trống tương tự, có lẽ được lấp đầy sơ sài. Điều sai lầm là có rất ít nội dung xảy ra trong suốt hai nghìn năm đó. Trong quyển sách này, những biện minh cho khoảng cách là những giới hạn về không gian và năng lực của tôi, và thực tế là chúng ta đang thăm dò những tiền thân trực tiếp cho những lập trường thời nay trong triết học toán học.]

[2] First Principles: những nguyên lý đầu tiên, xem như những khối xây dựng của kiến thức đúng thật. Một nguyên lý đầu tiên là một mệnh đề hoặc giả định nền tảng (vốn đứng riêng lẻ một mình). Chúng ta không thể suy ra những nguyên lý đầu tiên từ bất kỳ mệnh đề hoặc giả định nào khác. Aristotle, viết về những nguyên lý đầu tiên, nói: Trong mọi điều tra có hệ thống (methodos/phương pháp), ở đó có những nguyên lý, hay những nguyên nhân, hay những yếu tố đầu tiên, kiến thức và khoa học là kết quả từ việc thu nhận kiến thức của những điều này; vì chúng ta nghĩ rằng chúng ta biết một gì đó nếu là xảy ra rằng chúng ta có được kiến thức về những nguyên nhân chính, những nguyên lý đầu tiên lý chính, càng nhiều càng tốt hoặc hoàn toàn đến những yếu tố. Về sau, ông kết nối ý tưởng với kiến thức, định nghĩa những nguyên lý đầu tiên như ‘cơ sở đầu tiên từ đó một sự vật viêc thì được biết’.

[3] Immanuel Kant (1724-1804) là nhân vật trung tâm trong triết học hiện đại. Ông đã tổng hợp thuyết duy lý hiện đại ban đầu và thuyết duy nghiệm, đặt ra những thuật ngữ cho phần lớn triết học thế kỷ 19 và 20, và tiếp tục có ảnh hưởng đáng kể ngày nay trong siêu hình học, nhận thức học, đạo đức học, triết học chính trị, mỹ học và nhiều những lĩnh vực khác.

René Descartes (1596-1650) là một nhà toán học sáng tạo bậc nhất, một nhà tư tưởng khoa học quan trọng và một nhà siêu hình học ban đầu. Trong suốt cuộc đời của mình, trước nhất, ông là một nhà toán học, thứ hai là một nhà khoa học tự nhiên hay “triết gia tự nhiên”, và thứ ba là một nhà siêu hình học. Trong toán học, ông đã phát triển những kỹ thuật đưa đến hình học giải tích.

Isaac Newton (1642-1727) được biết đến nhiều nhất vì đã phát minh calculus, vào khoảng giữa đến cuối những năm 1660 (gần mười năm trước, độc lâp với Leibniz, và cuối cùng có ảnh hưởng lớn hơn) và vì đã xây dựng lý thuyết về lực hấp dẫn phổ quát – lý thuyết sau trong Principia của ông, công trình quan trọng nhất trong việc chuyển đổi triết học tự nhiên hiện đại ban đầu thành khoa học vật lý hiện đại.

Gottfried Wilhelm Leibniz (1646–1716), người Germany, là một trong những nhà tư tưởng vĩ đại của thế kỷ XVII và XVIII. Ông có những đóng góp sâu xa và quan trọng trong những lĩnh vực siêu hình học, nhận thức luận, logic học, triết học tôn giáo, cũng như toán học, vật lý học, địa chất học, luật học và lịch sử. Về toán học, ông nổi tiếng đã phát minh calculus (độc lập với Newton).

Baruch Spinoza (1632-1677), người Holland, gốc Jew, một trong những người đi đầu trong thuyết duy lý ở thế kỷ 17 và là một trong những nhân vật đầu tiên và nổi tiếng của thời kỳ Khai sáng. Tác phẩm của ông là Ethics (1677).

John Locke (1632-1704) triết gia người Britain, học giả Oxford và nhà nghiên cứu y học. An Essay Concerning Human Understanding (1689), công trình siêu việt nhiều ảnh hưởng của Locke, như một trong những tuyên ngôn biện minh lớn đầu tiên của thuyết duy nghiệm hiện đại, quan tâm với việc xác định những giới hạn của sự hiểu biết của con người với một loại nhiều đề tài. The Second Treatise of Government, tác phẩm chính trị nổi tiếng nhất của Locke, trong đó ông lập luận rằng chủ quyền nằm ở người dân và giải thích bản chất của chính phủ hợp pháp về quyền tự nhiên và khế ước xã hội. Ông cũng nổi tiếng với việc kêu gọi sự tách biệt giữa hội Nhà thờ và Nhà nước trong Letter Concerning Toleration.

George Berkeley (1685-1753), thày chăn chiên cấp tỉnh Cloyne, người Ireland, một trong những triết gia lớn của thời kỳ đầu hiện đại. Ông là nhà phê bình xuất sắc đối với những người đi trước, đặc biệt là với Descartes, Malebranche và Locke. Là nhà siêu hình học nổi tiếng, ông chủ trương một thuyết duy ý (tuyên bố rằng mọi sự vật việc hiện hữu đều hoặc là não thức hoặc phụ thuộc vào một não thức để hiện hữu, nên ông đôi khi được coi là cha đẻ của thuyết duy ý hiện đại) và thuyết phi-vật chất (tuyên bố rằng vật chất không hiện hữu). Ông cũng là nhân vật chính trong phong trào duy nghiệm của England, mặc dù thuyết duy nghiệm của ông thuộc loại rất cấp tiến, đến từ tuyên bố thường được nhắc nhở của ông ‘hiện hữu là được ý thức’.

David Hume (1711-1776): xem Hume – Đời Tôi, bản tôi dịch trên blog này.

Thomas Reid (1710-1796) triết gia người Scotland, ông bác bỏ thuyết duy nghiệm (nghiêng về) hoài nghi (skeptical Empiricism) của David Hume để ủng hộ một ‘triết lý của phán đoán hợp lý thực tiễn dựa trên khả năng nhận thức cơ bản thông thường có tổng quát với mọi người’ (philosophy of common sense) sau này được trường phái Scotland tán thành.

[4] infinitesimal calculus: nhánh toán học giải quyết với việc tìm kiếm và với những tính chất của đạo hàm và tích phân của những hàm số, bằng những phương pháp ban đầu dựa trên tổng số những hiệu số nhỏ, gần bằng không, tiến dần đến vô cực (infinitesimal differences). Hai loại calculus chính là phép tính vi phân và phép tính tích phân (differential calculus & integral calculus).

[5] Hume nêu lên sự khác biệt giữa ‘những quan hệ của ý tưởng’ và ‘những sự vật việc của thực tế’. Những quan hệ của những ý tưởng là những ràng buộc tiên nghiệm và không thể phá hủy, được tạo ra giữa những ý tưởng. Tất cả những phát biểu đúng lôgích như “5 + 7 = 12” và “tất cả những người độc thân đều không lập gia đình” đều là những quan hệ của những ý tưởng. Những quan hệ của những ý tưởng là về trực giác hay có thể chứng minh chắc chắn được, và một phủ nhận một mệnh đề như vậy có nghĩa là một mâu thuẫn.

Những vấn đề thực tế liên quan đến kinh nghiệm: ‘mặt trời chiếu sáng’, ‘hôm qua tôi đi dạo’, hay ‘ngày mai trời sẽ mưa’ đều là những sự vật việc của thực tế. Chúng được học hậu nghiệm, và có thể bị phủ nhận nhưng không sợ bị mâu thuẫn. Nếu bên ngoài trời đang nắng và tôi khẳng định rằng trời đang mưa, tôi có thể bị chứng minh là sai chỉ bằng việc nhìn ra cửa sổ và xem trời có mưa không: xác định của tôi không thể bị bác bỏ bằng chỉ đơn giản gọi đến lôgích và lý trí.

Trong khi tôi có thể biết nhiều những sự vật việc của thực tế từ kinh nghiệm giác quan hoặc từ trí nhớ, nhưng nguồn kiến thức của tôi không phải là bạn tôi đang ở France hay mặt trời sẽ mọc vào ngày mai. Hume nêu lên rằng chúng ta biết những vấn đề thực tế của những sự vật việc chưa được quan sát qua một tiến trình nhân quả. Sự hiểu biết của tôi rằng bạn tôi đang ở France có thể là từ một lá thư gây ra hậu quả đó, và kiến thức của tôi rằng mặt trời sẽ mọc vào ngày mai được suy ra từ kinh nghiệm trong quá khứ, vốn cho tôi biết mặt trời đã mọc mỗi ngày trong quá khứ.

[6] Sự phân biệt ‘phân tích / tổng hợp’ nói về một phân biệt giữa hai loại của sự đúng thật. Những đúng thật tổng hợp đều đúng vì (a) những gì chúng có nghĩa, và (b) vì cách thức là-thế của thế giới, trong khi những đúng thật phân tích đều đúng chỉ vì những gì chúng có nghĩa mà thôi. Thí dụ: “Tuyết thì trắng” là tổng hợp, vì nó thì đúng thật, phần vì nghĩa của nó (mênh đề phát biểu) và phần vì tuyết (cách thức của thế giới) có một màu sắc nhất định. Ngược lại, “Tất cả những người độc thân đều chưa-lập gia đình”, thường được cho là đúng bất kể cách thức thế giới là như thế nào; nó là ‘đúng nhờ vào ý nghĩa’," hoặc do phân tích. Sự hiện hữu của những đúng thật phân tích vẫn còn tranh luận chưa ngã ngũ. Những triết gia từng nghĩ rằng chúng hiện hữu gồm Immanuel Kant, Gottlob Frege và Rudolf Carnap. Nhà triết học nổi tiếng nhất với suy nghĩ rằng chúng không hiện hữu là W. V. V. O. Quine. Những người hoài nghi đôi khi cho rằng ý tưởng về những đúng thật phân tích là không mạch lạc và đôi khi họ bày tỏ điều này qua việc phủ nhận sự tồn tại của sự khác biệt giữa phân tích & tổng hợp’. Một quan điểm liên quan là tuy có một sự khác biệt nhưng nó thì không đáng kể, vì lớp gồm những mệnh đề phân tích thì trống. Một loại hoài nghi thứ ba về khả năng phân tích đặt câu hỏi về tính hữu dụng của nó.

[7] [Khái niệm được diễn tả bằng từ tiếng England ‘triangle’ chứa đựng khái niệm của là ‘có ba-góc’. Nó cũng chứa khái niệm cua ‘ba mặt’? Từ tiếng Germany cho tam giác là Dreieck, hay ba-góc. Có lẽ, khái niệm đó gồm ba-góc, nhưng, lại nữa, nó có gồm ba-cạnh không?]

[8] [Là khó khăn để xác định về thí dụ này vì, theo như tôi biết, Kant không nói về chứng minh trong số học. Ông có đồng ý rằng một số luật trong số học là phân tích, nhưng có lẽ chúng ta cần trực giác để xác định rằng không phải mọi số nguyên tố lớn hơn 100 đều là hợp số. Điểm nói ở đây là ông sẽ chắc chắn sẽ chủ trương rằng chúng ta cần trực giác để thiết lập tuyên bố về sự hiện hữu. Trong những hệ thống lôgích thời nay, ‘không là trường hợp rằng tất cả x là P’ theo đến rằng ‘có một x vốn không-P’. Trong những ký hiệu, ¬ ∀xPx dẫn đến ∃3x ¬ Px. Để đi vào vào một chủ trương lỗi thời thô sơ, nếu cách giải thích ở trên của Kant là đúng, thì người ấy sẽ coi suy luận này liên quan đến trực giác. Đó là, suy luận được nói đến có thể dẫn từ một đúng thật phân tích đến một đúng thật tổng hợp. Xem Posy 1984 cho một giải thích có ý nghĩ về lôgích thích hợp để gán cho Kant].

[9] incommensurable, dẫn đến số vô tỉ

[10] contingent: tùy thuôc (vào trường hợp/mệnh đề) có khi là đúng và có khi là sai, (ngược với necessary: tất yếu)

[11] spatio-temporal

[12] individual

[13] Universal generalization hay universal introduction (∀I, đôi khi là GEN) là một quy tắc cơ bản của suy diễn trong logic bậc nhất (first-order logic) mà theo đó một phát biểu phổ quát được đưa vào một chứng minh. Quy tắc tổng quát hóa phổ quát chủ trương rằng nếu bạn có thể chứng minh một sự việc gì là đúng với bất kỳ hằng số tùy tiện nào, thì nó phải là đúng với mọi sự biệc. Điều này cho phép bạn chuyển từ một tuyên bố cụ thể về một đối tượng tùy tiện bất kỳ sang một tuyên bố tổng quát bằng việc dùng một biến số định lượng. Quy tắc giới thiệu phổ quát có thể được trình bày chính thức như sau:

If Γ φ(c), then Γ ∀xφ(x)

… trong đó Γ là một tập hợp những công thức và c là một hằng số tùy tiện vốn mới với chứng minh hoặc lập luận đang được trình bày. Tức là hằng số c không thể có trong Γ.

[14] [Về khái niệm tam giác, xem chú thích 2 ở trên.]

[15] in concreto

[16] [Mệnh đề 32 là: ‘Trong một tam giác bất kỳ, nếu một trong những cạnh được tạo ra, góc ngoài thì bằng hai góc nội tiếp và những góc đối diện, và ba góc trong của tam giác thì bằng hai góc vuông’. Như thế, cắm mốc sẽ là tam giác ABC dọc theo với đoạn thẳng BD. Xây dựng phụ là đoạn thẳng BE song song với AC.]

[17] [Vấn đề này có liên quan đến một trong những cái gọi là ‘những khoảng trống’ lôgích trong Elements của Euclid. Giả định rằng chúng ta có một đường thẳng đi từ bên trong của một đường tròn ra bên ngoài. Euclid giả định rằng có một điểm vốn đường thẳng cắt đường tròn. Theo cái nhìn thời nay, điều này không tuân theo những định đề, tiên đề và định nghĩa. Người ta phải rành mạch thêm vào một nguyên lý của tính liên tục. Tuy nhiên, nếu chúng ta coi suy luận của Euclid như được trực giác hướng dẫn, khi đó có lẽ không có khoảng trống. Từ viễn tượng này, tính liên tục của đường tròn và đường thẳng là trực giác , và không mang tính lôgích hay phân tích.]

[18] [những định lý số học trong Sách 10 Elements của Euclid được giải thích rõ ràng bằng những thuật ngữ hình học. Một số nhà bình luận gán cho Kant một nền tảng tiên đề về số học. Ngẫu nhiên, tôi không biết Kant sẽ tạo ra sự khác biệt gì, như 12 – 5 = 7. Người ta có thể nghĩ rằng không cần xây dựng phụ trợ ở đây. Khi chúng ta đã nắm được khái niệm về mười hai đối tượng, chúng ta có thể mổ xẻ nó để xác định sự khác biệt. Mặt khác, có lẽ chính hành động phân vùng sưu tập là một công trình liên quan đến trực giác.]

[19] [Tuy nhiên, định đề thứ tư của Euclid là ‘tất cả những góc vuông đều bằng nhau’, điều này không đại diện cho một xây dựng.]

[20] projective

[21] [Một số nhà giải thích nói Kant chủ trương rằng người ta không thể diễn đạt những khái niệm của hình học với không gọi đến sự xây dựng trong trực giác – và xây dựng này là theo Euclid. Vì vậy, ngay cả hình học không-Euclid cũng giả định trước tính tất yếu của hình học theo Euclid.]

[22] the analyticity of mathematics

[23]John Stuart Mill (1806–73) là nhà triết học tiếng England có ảnh hưởng nhất trong thế kỷ XIX. Ông là một nhà tự tưởng theo thuyết duy nhiên (natualist), một người theo thuyết duy lợi thực dụng (utilitarianism), và một người theo chủ nghĩa tự do, với những tác phẩm khám phá những hệ quả của một quan điểm theo chủ nghĩa kinh nghiệm trọn vẹn triệt để. Trong việc làm như vậy, ông đã tìm kết hợp những gì hay nhất của tư tưởng Khai sáng thế kỷ 18 với những trào lưu triết học lịch sử và phong trào lãng mạn mới xuất hiện của thế kỷ 19. Những tác phẩm quan trọng nhất của ông gồm System of Logic (1843), On Liberty (1859), Utilitarianism (1861) and An Examination of Sir William Hamilton’s Philosophy (1865).

[24] transcendentalism

[25] foundationalism

[26] [Xem chương 1, §3 để biết sơ lược về thuyết duy nhiên trong triết học toán học. Maddy 1997 là một nghiên cứu thông xuốt.]

[27] Rudolf Carnap (1891–1970) triết gia người Germany, là một trong những nhà triết học nổi tiếng nhất của thế kỷ XX. Carnap là một trong những người khởi xướng của lĩnh vực mới về triết học khoa học và sau này là người đóng góp đứng đầu cho ngữ nghĩa học và lôgic quy nạp.Nổi tiếng là một trong những người sáng lập, và có lẽ là đại diện đứng đầu về triết học của phong trào được biết như chủ nghĩa thực chứng lôgic hay chủ nghĩa thực nghiệm logic (logical empiricism/logical positivism).

Ông là triết gia dẫn đầu của NhómVienna (Vienna Circle) vào cuối những năm 1920 và đầu những năm 1930. Lần đầu tiên ông được biết đến nhiều với quyển Der logische Aufbau der Welt, 1928. Quyển sách lớn tiếp theo của ông, Logical Syntax of Language (Cú pháp logic của ngôn ngữ),1934, đã tìm cách giải quyết tranh luận giữa những trường phái cơ bản của thuyết logic, thuyết trực giác và thuyết hình thức (lúc đó đang ở đỉnh cao của nó) bằng đề nghị một ‘nguyên tắc khoan dung’, theo đó không có lôgic ‘đúng’ cuối cùng, nhưng chỉ có những lôgic ít hay nhiều hữu ích hơn cho những mục đích khác nhau của con người. Điều này đã trở thành nguyên tắc dẫn đường cho toàn bộ triết lý sau này của ông, bao gồm chương trình “giải thích” của ông, hay thay thế từng phần những ý tưởng và khái niệm mơ hồ bằng những ý tưởng và khái niệm tốt hơn. Quyển sách lớn khác của ông là Logical Foundations of Probability,1950, đã định hình lại lĩnh vực và cuối cùng dẫn đến nhận thức luận Bayes hiện tại (Bayesian epistemology) và thuyết quyết định (decision theory).

[28] Enumerative Induction: Quy Nạp Liệt Kê – phương pháp quy nạp trong đó kết luận được xây dựng dựa trên số lượng của những trường hợp hỗ trợ nó. Càng nhiều trường hợp hỗ trợ, kết luận càng vững mạnh.

[29] [Lưu ý sự giống nhau giữa những khái niệm giới hạn của Mill và cách những giới hạn, như đạo hàm và nguyên hàm, được định nghĩa trong tích phân thời nay.]

[30] tâm vòng tròn ngoại tiếp

[31] [Như Frege đã lưu ý trong một nội dungkhác, suy diễn những tổng số của Mill làm việc dùng luật kết hợp là thiết yếu]

[32] [Giải quyết của Mill về tính tất yếu hiển nhiên và tiên nghiệm của toán học thì tương tự với luận điểm của Hume về tính nhân quả và ‘liên hệ tất yếu’. Hume đề nghị rằng tin tưởng của chúng ta vốn một điều này gây ra một điều kia thì dựa trên kinh nghiệm không đổi của chúng ta về hai điều xảy ra cùng nhau, đến mức khi chúng ta nhìn thấy một trong chúng xảy ra, chúng ta mong đợi điều kia sẽ xảy ra. Xem Yablo 1993 cho một thảo luận sâu xa về mức độ vốn tính có thể mường tượng là một hướng dẫn đáng tin cho tính có thể có được. Một số kết quả của vật lý thời nay cho thấy rằng có lẽ vũ trụ vận hành theo những cách vốn chúng ta thấy không thể tưởng tượng được. Điều này có đem cho sự phủ nhận thực nghiệm về mức độ tin cậy của trực giác không gian và thời gian không? Nếu cuối cùng chúng ta không thể dựa vào ‘kinh nghiệm sớm có và kông đổi’, khi đó một người theo Mill có thể dựa trên gì?]

[33] Tiên đề bao hàm (comprehension axiom)

Saturday, April 23, 2022

Shapiro – Suy Nghĩ Về Toán Học (04)